
如果抛物线y=ax2+5的顶点是它的最低点,那么a的取值范围是_____.
a>0 【解析】根据二次函数的图像,由抛物线y=ax2+5的顶点是它的最低点,知a>0, 故答案为a>0.科目:初中数学 来源:江苏省苏州市姑苏区2017~2018学年第一学期八年级数学期末考试试卷 题型:单选题
如图,已知△ABC中,∠A=75°,则∠1+∠2=( )
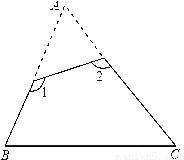
A. 335°° B. 255° C. 155° D. 150°
B 【解析】∵∠A+∠B+∠C=180°,∠A=75°, ∴∠B+∠C=180°﹣∠A=105°. ∵∠1+∠2+∠B+∠C=360°, ∴∠1+∠2=360°﹣105°=255°. 故选B.查看答案和解析>>
科目:初中数学 来源:广东省潮州市潮安区2017-2018学年八年级上学期期末教学质量检测数学试卷 题型:填空题
从多边形的一个顶点出发引对角线,可以把这个多边形分割成7个三角形,则该多边形为 边形。
九 【解析】 试题分析:多边形的边数=7+2=9.查看答案和解析>>
科目:初中数学 来源:2018年上海市奉贤区中考数学一模试卷 题型:解答题
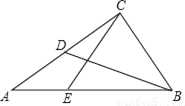
已知:如图,在Rt△ABC中,∠ACB=90°,BC=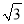 ,cot∠ABC=
,cot∠ABC=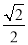 ,点D是AC的中点.
,点D是AC的中点.
(1)求线段BD的长;
(2)点E在边AB上,且CE=CB,求△ACE的面积.
查看答案和解析>>
科目:初中数学 来源:2018年上海市奉贤区中考数学一模试卷 题型:填空题
如果两个相似三角形的面积的比是4:9,那么它们对应的角平分线的比是_____.
2:3 【解析】先根据相似三角形面积的比是4:9,求出其相似比是2:3,再根据其对应的角平分线的比等于相似比,可知它们对应的角平分线比是2:3. 故答案为:2:3.查看答案和解析>>
科目:初中数学 来源:2018年上海市奉贤区中考数学一模试卷 题型:单选题
设n为正整数, 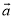 为非零向量,那么下列说法不正确的是( )
为非零向量,那么下列说法不正确的是( )
A. n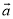 表示n个
表示n个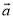 相乘 B. -n
相乘 B. -n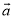 表示n个-
表示n个-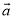 相加
相加
C. n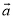 与
与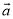 是平行向量 D. -n
是平行向量 D. -n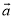 与n
与n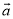 互为相反向量
互为相反向量
查看答案和解析>>
科目:初中数学 来源:四川省自贡市2016-2017学年上学期九年级期末统一考试数学试卷 题型:解答题
如图, 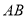 是⊙
是⊙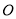 的直径,
的直径, 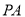 是⊙
是⊙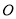 的切线,
的切线, 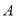 是切点,
是切点, 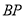 与⊙
与⊙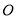 交于点
交于点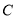 .
.
(1).若AB=4,∠ABP=60°,求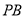 的长;
的长;
(2).若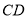 是⊙
是⊙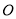 的切线.求证:
的切线.求证: 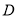 是
是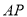 的中点.
的中点.

查看答案和解析>>
科目:初中数学 来源:四川省自贡市2016-2017学年上学期九年级期末统一考试数学试卷 题型:单选题
⊙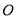 是△
是△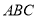 的外接圆,
的外接圆, 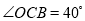 ,则
,则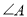 的度数是( )
的度数是( )

A. 40° B. 50° C. 60° D. 100°
B 【解析】∵, ∴ ;由圆周角定理可求: .故选B.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com