
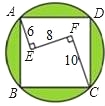
��ͼ����������ABCD����һ���߶Σ�����AE�AEF��EF�AFC������AE=6��EF=8��FC=10�����������������Բ֮���γɵ���Ӱ���ֵ����Ϊ ��

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ������ʡ�����ػ�ͤ��2017~2018ѧ����꼶��ѧ���ϣ���ĩ�ۺϼ��ģ���� ���ͣ������
�������鲿�ų�������ijƷ�Ƶ�����Ʒ�Ĵ�Ʒ��Ϊ5%��һλ�������������ֲ�Ʒ1000�����������д�Ʒ��_______����
50 ��������1000��5%=50�����ʴ�Ϊ50���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡ�����2018����꼶��ѧ������������ѧ�Ծ���Word�棩. ���ͣ������
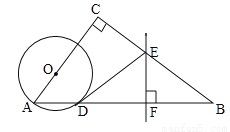
��ͼ���ڡ�ABC�У���C=90�㣬��O��AC�ϣ���OAΪ�뾶�ġ�O��AB�ڵ�D��BD�Ĵ�ֱƽ���߽�BC�ڵ�E����BD�ڵ�F������DE��
��1���ж�ֱ��DE���O��λ�ù�ϵ����˵�����ɣ�
��2����AC=6��BC=8��OA=2�����߶�DE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡ�����2018����꼶��ѧ������������ѧ�Ծ���Word�棩. ���ͣ���ѡ��
.��3��4Ϊ���߳��������εĵ����߳��Ƿ���x2-13x+40=0�ĸ�������������ε��ܳ�Ϊ�� ��
A. 15��12 B. 12 C. 15 D. ���϶�����
B ������������������ߣ��࣬��ã� �� ���������εĵ����߳�Ϊx��������ã�4��3��x��4+3�����1��x��7����x=5���������ܳ�Ϊ3+4+5=12����ѡB���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017��ӱ�ʡ�п���ѧģ���Ծ� ���ͣ������
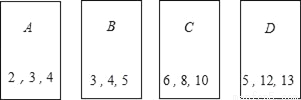
�����ű��ΪA��B��C��D�Ŀ�Ƭ��������⣬������ȫ��ͬ��������ֱ�д����ͼ��ʾ���������������ϣ�ϴ�ȷźã�
��1������֪��������a2+b2=c2������������a��b��c��Ϊ���������μδ��������ȡһ�ţ���鵽�Ŀ�Ƭ�ϵ����ǹ������ĸ���P1��
��2���������������ȡһ�ţ����Żأ����ٴ�ʣ�µĿ�Ƭ�������ȡһ�ţ���Ƭ��A��B��C��D��ʾ���������б�������ͼ�ķ�����鵽�����ſ�Ƭ�ϵ������ǹ������ĸ���P2����ָ������μγ鵽�������Ŀ�����һ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017��ӱ�ʡ�п���ѧģ���Ծ� ���ͣ���ѡ��
��֪a��b�Ƿ���x2+2013x+1=0������������1+2015a+a2����1+2015b+b2����ֵΪ��������
A. 1 B. 2 C. 3 D. 4
D ����������Ϊa��b�Ƿ���x2+2013x+1=0��������������ab=1��-a2-2013a=1��-b2-2013b=1�����ԣ�1+2015a+a2����1+2015b+b2��=��-a2-2013a+2015a+a2����-b2-2013b+2015b+b2��=4ab=4.��ѡD.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017��ӱ�ʡ�п���ѧģ���Ծ� ���ͣ���ѡ��
ʹ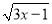 �������x��ȡֵ��Χ�ǣ�������
�������x��ȡֵ��Χ�ǣ�������
A. x> B. x>-
B. x>- C. x��
C. x�� D. x��-
D. x��-
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017������ʡӪ���д�ʯ����ˮԴ����һ����ѧУ�п���ѧģ���Ծ� ���ͣ������
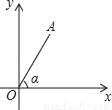
��ͼ����A��t��4���ڵ�һ���ޣ�OA��x�����е����Ϊ����tan��=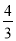 ����t��ֵΪ_____��
����t��ֵΪ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���ӱ�ʡ��ɽ��·����2017���п���ѧ��ģ�Ծ��������棩 ���ͣ������
��ͼ����Rt��ABC�У���ACB=90�㣬AC=6��BC=8������B������BB1��AC������D�ӵ�A����������AC������ÿ��5����λ���ٶ��˶���ͬʱ����E�ӵ�C����������AC������ÿ��3����λ���ٶ��˶�������D��DH��AB��H������E��EF��AC������BB1��F������DF�����˶���ʱ��Ϊt�루t��0����
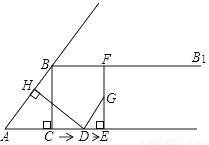
��1����tΪ________ʱ��AD=AB����ʱDE�ij���Ϊ________��
��2������DEF���ACBȫ��ʱ����t��ֵ��
��3����DH����ֱ��Ϊ�Գ��ᣬ�߶�AC����ԳƱ任���ͼ��ΪA��C�䣮
�ٵ�t��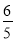 ʱ�����ADA������ΪS��ֱ��д��S����t�ĺ�����ϵʽ��
ʱ�����ADA������ΪS��ֱ��д��S����t�ĺ�����ϵʽ��
�ڵ��߶�A��C��������BB1�й�����ʱ����t��ȡֵ��Χ��
��1��2��2����2��t=6����3����S=12t2���� . �����������������(1)������Rt��ABC�Ĺ��ɶ������AB=10������AD=AB�ó�t��ֵ�������������CD�ij��ȣ�Ȼ�����DE=CE-CD����𰸣�(2)�����ȸ�������ó��ı���BCEFΪ���Σ��������������AD��AEʱ���t��ȡֵ��Χ��Ȼ����ݡ�ACB�͡�DEFȫ�ȵó�t��ֵ����AD��AEʱ���t��ȡֵ��Χ��Ȼ����ݡ�ACB��...�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com