
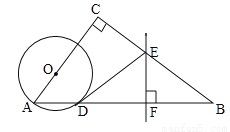
��ͼ���ڡ�ABC�У���C=90�㣬��O��AC�ϣ���OAΪ�뾶�ġ�O��AB�ڵ�D��BD�Ĵ�ֱƽ���߽�BC�ڵ�E����BD�ڵ�F������DE��
��1���ж�ֱ��DE���O��λ�ù�ϵ����˵�����ɣ�
��2����AC=6��BC=8��OA=2�����߶�DE�ij���
 �ݾ�ѵ������ϵ�д�
�ݾ�ѵ������ϵ�д� С����ȫ�ܼ��ϵ�д�
С����ȫ�ܼ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ���㽭ʡ������2017-2018ѧ����꼶�ϲ���ĩģ����ѧ�Ծ� ���ͣ������
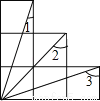
��ͼΪ6���߳���ȵ������ε����ͼ�Σ����1+��2+��3= ___________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�����ʡ�������п���ѧģ���Ծ� ���ͣ������
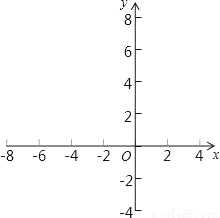
��֪������y=ax2+bx+c��x�ύ��A��B���㣬��y�ύ�ڵ�C�����е�B��x����������ϣ���C��y����������ϣ��߶�OB��OC�ij���OB��OC���Ƿ���x2��10x+16=0�����������������ߵĶԳ�����ֱ��x=��2��
��1����A��B��C��������ꣻ
��2����������ߵı���ʽ��
��3������AC��BC������E���߶�AB�ϵ�һ�����㣨���A����B���غϣ�������E��EF��AC��BC�ڵ�F������CE����AE�ij�Ϊm����CEF�����ΪS����S��m֮��ĺ�����ϵʽ����д���Ա���m��ȡֵ��Χ��
��4���ڣ�3���Ļ�������˵��S�Ƿ�������ֵ�������ڣ������S�����ֵ���������ʱ��E�����꣬�жϴ�ʱ��BCE����״���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�����ʡ�������п���ѧģ���Ծ� ���ͣ���ѡ��
������ε����Ľ�����������һ���ڽǵĹ�ϵ�ǣ�������
A. ���� B. ���� C. ����� D. ����ȷ��
B ����������������εı���Ϊn����������ε����Ľ�Ϊ��������ε�һ����ǵ��ڣ�����������ε����Ľǵ���������ε�һ����ǣ���������ε�һ������������������ڵ�һ���ڽǵĻ���������������ε����Ľ�����������һ���ڽǻ����� ��ѡB���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�����ʡ�������п���ѧģ���Ծ� ���ͣ���ѡ��
�����߶��У��ܳɱ������ǣ�������
A. 3cm��6cm��8cm��9cm B. 3cm��5cm��6cm��9cm
C. 3cm��6cm��7cm��9cm D. 3cm��6cm��9cm��18cm
D ����������������߶εij˻��������������߶εij˻������������߶ν����ɱ����߶�.�������ѡ���У�ֻ��D���ϣ�3��18=6��9����ѡD.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡ�����2018����꼶��ѧ������������ѧ�Ծ���Word�棩. ���ͣ������
���ʵ��ķ����ⷽ��
��1����3x-1��2=4��2x-3��2��
��2��x2-3x-10=0��
��3��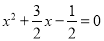 ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡ�����2018����꼶��ѧ������������ѧ�Ծ���Word�棩. ���ͣ���ѡ��
��ͼ��AB�ǰ�Բ�뾶���뾶OC��AB�ڵ�O����D�ǻ�BC���е㣬����CD��AD��OD�����������ĸ����ۣ��١�DOB=��ADC����CE=OE���ۡ�ODE�ס�ADO����2CD2=CE��AB��������ȷ���۵�����ǣ�������
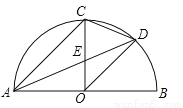
A. �٢� B. �ڢ� C. �٢� D. �٢ڢ�
C ������������������١�AB�ǰ�Բֱ������AO=OD�����OAD=��ADO����ADƽ�֡�CAB����BC�ڵ�D�� ���CAD=��DAO=��CAB�� ���CAD=��ADO�� ��AC��OD�� ���DOB=��CAO���֡ߡ�CAO=��ADC�������Ű�Բ���������DOB=��ADC�ʢ���ȷ�� ��������ã�OD=R��AC=R�� ��OE��CE=OD��AC=1�� �� ��OE��CE���ʢڴ���...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017��ӱ�ʡ�п���ѧģ���Ծ� ���ͣ������
��ͼ����������ABCD����һ���߶Σ�����AE�AEF��EF�AFC������AE=6��EF=8��FC=10�����������������Բ֮���γɵ���Ӱ���ֵ����Ϊ ��
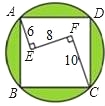
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017������ʡӪ���д�ʯ����ˮԴ����һ����ѧУ�п���ѧģ���Ծ� ���ͣ���ѡ��
У���������10˫�˶�Ь�ij���ͳ�������
���루cm�� | 25 | 25.5 | 26 | 26.5 | 27 |
��������˫�� | 1 | 1 | 2 | 4 | 2 |
����10˫�˶�Ь�������������λ���ֱ�Ϊ��������
A. 4cm��26cm B. 4cm��26.5cm
C. 26.5cm��26.5cm D. 26.5cm��26cm
C ������������λ��Ҫ�����ݴ�С�����˳�����У�λ�����м��һ����������������ƽ������Ϊ��λ����������һ�������г��ִ����������ݣ�ע���������Բ�ֹһ��. �������� ����һ��������26.5�dz��ִ������ģ���������26.5cm�� �������������м�λ�õ�����26.5��26.5����ô��λ���Ķ����֪���������ݵ���ֱ��˽�ǣ�26.5+26.5����2=26.6cm. ��ѡC. ...�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com