
为了解青少年形体情况,现随机抽查了若干名初中学生坐姿、站姿、走姿的好坏情况(如果一个学生有一种以上不良姿势,以他最突出的一种作记载),并将统计结果绘制了如下两幅不完整的统计图,请根据图中所给信息解答下列问题:
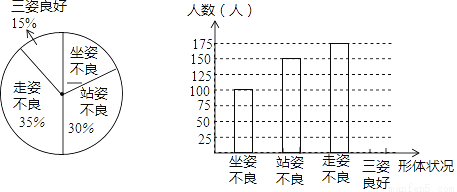
(1)求这次被抽查形体测评的学生一共有多少人?
(2)求在被调查的学生中三姿良好的学生人数,并将条形统计图补充完整;
(3)若全市有5万名初中生,那么估计全市初中生中,坐姿和站姿不良的学生共有多少人?
【答案】(1)500名;(2)75名;(3)2.5万
【解析】试题分析:(1)用类型人数除以所占百分比就是总人数.(2)用总人数乘以15%.
(3) 坐姿和站姿不良的学生的学生的百分比乘以总人数.
试题解析:
(1)【解析】
100÷20%=500(名),
答:这次被抽查形体测评的学生一共是500名;
(2)【解析】
三姿良好的学生人数:500×15%=75名,
补全统计图如图所示;
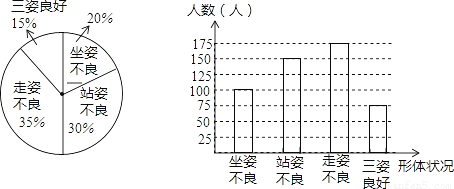
(3)【解析】
5万×(20%+30%)=2.5万,
答:全市初中生中,坐姿和站姿不良的学生有2.5万人.
【题型】解答题
【结束】
24
如图,矩形ABCD中,P为AD边上一点,沿直线BP将△ABP翻折至△EBP(点A的对应点为点E),PE与CD相交于点O,且OE=OD.
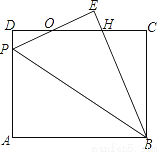
(1)求证:PE=DH;
(2)若AB=10,BC=8,求DP的长.
(1)见解析;(2). 【解析】试题分析:(1) 先证明△DOP≌△EOH,再利用等量代换得到PE=DH. (2) 设DP=x, Rt△BCH中,先用 x表示三角形三边,利用勾股定理列式解方程. 试题解析: (1)【解析】 证明:∵OD=OE,∠D=∠E=90°,∠DOP=∠EOH, ∴△DOP≌△EOH, ∴OP=OH, ∴PO+OE=OH+OD, ... 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:初中数学 来源:2016-2017学年陕西省七年级(下)第二次测验数学试卷 题型:单选题
若单项式 的系数是m,次数是n,则mn的值为( )
的系数是m,次数是n,则mn的值为( )
A. ﹣2 B. ﹣6 C. ﹣4 D. 
查看答案和解析>>
科目:初中数学 来源:安徽省16-17学年度第一学期七年级数学期末考试卷 题型:单选题
若使等式(-4)□(-6)=2成立,则□中应填入的运算符号是( )
A. + B. - C. × D. ÷
B 【解析】利用运算法则计算即可确定出运算符号. 【解析】 根据题意得,(-4)-(-6)=-4+6=2, 故选B.查看答案和解析>>
科目:初中数学 来源:山西农业大学附属中学2017-2018学年八年级上学期第三次月考数学试卷 题型:单选题
如图,Rt△ABC中,∠C=90°,∠B=45°,AD是∠CAB的平分线,DE⊥AB于E,AB=a,CD=m,则AC的长为
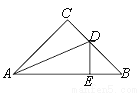
A. 2m B. a﹣m C. a D. a+m
B 【解析】:∵AD是∠CAB的平分线,DE⊥AB,∠C=90°, ∴CD=DE, 在Rt△ACD和Rt△AED中, , ∴Rt△ACD≌Rt△AED(HL), ∴AC=AE, ∵∠B=45°,DE⊥AB, ∴△BDE是等腰直角三角形, ∴BE=DE=m, ∵AE=AB-BE=a-m, ∴AC=a-m. 故选B.查看答案和解析>>
科目:初中数学 来源:山西农业大学附属中学2017-2018学年八年级上学期第三次月考数学试卷 题型:单选题
下列“数字”图形中,有且仅有一条对称轴的是
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源:黑龙江省哈尔滨市香坊区2017年中考数学二模试卷(解析版) 题型:填空题
如图,在⊙O中,AC是弦,AD是切线,CB⊥AD于B,CB与⊙O相交于点E,连接AE,若AE平分∠BAC,BE=1,则CE=________.
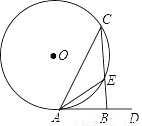
【答案】2
【解析】∵AD是切线,  ∠EAB=∠C,
∠EAB=∠C,
∵AE是角平分线,
∠CAE=∠EAB,
 ∠CAE=∠EAB=∠C,
∠CAE=∠EAB=∠C,
∵CB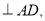
 ∠C+∠CAB=90°,
∠C+∠CAB=90°,
 3∠C=90°,
3∠C=90°,
 ∠C=30°.
∠C=30°.
故答案为30°.
【题型】填空题
【结束】
19
在?ABCD中(非矩形),连接AC,△ABC为直角三角形,若AB=4,AC=3,则AD=________.
或5 【解析】(1)如图,四边形是平行四边形,利用勾股定理知,CD=AB,AD= (2) 四边形是平行四边形,利用勾股定理知,BC=AD=.查看答案和解析>>
科目:初中数学 来源:黑龙江省哈尔滨市香坊区2017年中考数学二模试卷(解析版) 题型:填空题
103 000用科学记数法表示为________.
【答案】1.03×105
【解析】103 000=1.03×105
故答案为1.03×105.
【题型】填空题
【结束】
12
当x=________时,分式 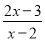 的值为1
的值为1
查看答案和解析>>
科目:初中数学 来源:江西省抚州市2017-2018年上学期九年级数学期末试卷 题型:解答题
有A、B两组卡片共5张,A组的三张分别写有数字2,4,6,B组的两张分别写有3,5.它们除了数字外没有任何区别,
(1)随机从A组抽取一张,求抽到数字为2的概率;
(2)随机地分别从A组、B组各抽取一张,请你用列表或画树状图的方法表示所有等可能的结果.现制定这样一个游戏规则:若选出的两数之积为3的倍数,则甲获胜;否则乙获胜.请问这样的游戏规则对甲乙双方公平吗?为什么?
(1)【解析】 P(抽到数字为2)=;(2)不公平,理由见解析. 【解析】试题分析:(1)根据概率的定义列式即可;(2)画出树状图,然后根据概率的意义分别求出甲、乙获胜的概率,从而得解. 试题解析: (1)P=; (2)由题意画出树状图如下: 一共有6种情况, 甲获胜的情况有4种,P=, 乙获胜的情况有2种,P=, 所以,这样的游戏规则对甲乙双方不公平....查看答案和解析>>
科目:初中数学 来源:2017年甘肃省兰州市中考数学模拟试卷 题型:解答题
如图,抛物线y=ax2+bx﹣4与x轴交于A(4,0)、B(﹣2,0)两点,与y轴交于点C,点P是线段AB上一动点(端点除外),过点P作PD∥AC,交BC于点D,连接CP.
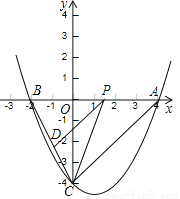
(1)求该抛物线的解析式;
(2)当动点P运动到何处时,BP2=BD•BC;
(3)当△PCD的面积最大时,求点P的坐标.
(1);(2)(,0);(3)(1,0) 【解析】 试题分析:(1)由抛物线y=ax2+bx﹣4过点A(4,0)、B(﹣2,0)根据待定系数法求解即可; (2)设点P运动到点(x,0)时,有BP2=BD•BC,在中,令x=0时,则y=﹣4,即可求得点C的坐标,由PD∥AC可得△BPD∽△BAC,再根据相似三角形的性质求解即可; (3)由△BPD∽△BAC,根据相似三角形的性...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com