
不透明的口袋里装有白、黄、蓝三种颜色的乒乓球(除颜色外其余都相同),其中白球有2个,黄球有1个,现从中任意摸出一个是白球的概率为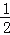 .
.
(1)试求袋中蓝球的个数;
(2)第一次任意摸一个球(不放回),第二次再摸一个球,请用画树状图或列表格法,求两次摸到都是白球的概率.
(1)1个(2)1/6 【解析】试题分析:(1)先根据白球的概率是,可求出球的总数,然后用求得的球的总个数减去白球和黄球的个数即可; (2)画出树状图可知,共有12种可能结果,两次摸到的球都为白球的情况有2种,从而可求出两次摸到的球都是白球的概率. 【解析】 (1)总球数为个,4-2-1=1 ∴蓝球有1个 (2) 开始 第一次 白1 白2 黄 蓝 第二次... 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案科目:初中数学 来源:江苏省盐城市2016-2017学年八年级上学期期末考试数学试卷 题型:填空题
如图,在?ABCD中,E为边CD上一点,将△ADE沿AE折叠至△AD′E处,AD′与CE交于点F.若∠B=52°,∠DAE=20°,则∠FED′的大小为________.
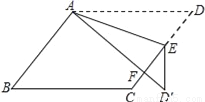
查看答案和解析>>
科目:初中数学 来源:安徽省2017~2018学年上学期九年级数学期末试卷 题型:解答题
袋中有外观相同的红球和白球各1个,随机摸出一球记下颜色,放回摇匀后,再随机摸出一球,求两次摸到球的颜色相同的概率是多少?(先画树状图或列表格,再求概率)
【解析】试题分析:首先根据题意画出树状图,然后由树状图求得所有等可能的结果与小明两次摸出的球颜色相同的情况,再利用概率公式即可求得答案. 试题解析: 画树状图得: ∵共有4种等可能的结果,两次摸到的球的颜色相同的有2种情况, ∴两次摸到的球的颜色相同的概率为: .查看答案和解析>>
科目:初中数学 来源:安徽省2017~2018学年上学期九年级数学期末试卷 题型:单选题
三角形两边的长分别是8和6,第三边的长是一元二次方程x2﹣16x+60=0的一个实数根,则该三角形的面积是( )
A. 24 B. 24或8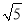 C. 48 D. 8
C. 48 D. 8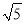
查看答案和解析>>
科目:初中数学 来源:安徽省2017-2018学年九年级上学期期末试卷数学 题型:解答题
某宾馆有50个房间供游客居住,当每个房间定价120元时,房间会全部住满,当每个房间每天的定价每增加10元时,就会有一个房间空闲,如果游客居住房间,宾馆需对每个房间每天支出20元的各种费用,设每个房间定价增加10x元(x为整数).
(1)直接写出每天游客居住的房间数量y与x的函数关系式;
(2)设宾馆每天的利润为W元,当每个房间定价为多少元时,宾馆每天所获利润最大,最大利润是多少?
(3)某日,宾馆了解当天的住宿情况,得到以下信息:
①当日所获利润不低于5000元,
②宾馆为游客居住的房间共支出费用没有超过600元,
③每个房间刚好住满2人.
问:这天宾馆入住的游客人数最少有多少人?
(1)y=50-x,(0≤x≤50,且x为整数);(2)每间房价定价为320元时,宾馆每天所获利润最大,最大利润是9000元;(3)20人 【解析】试题分析:(1)根据每天游客居住的房间数量等于50﹣减少的房间数即可解决问题. (2)构建二次函数,利用二次函数的性质解决问题. (3)根据条件列出不等式组即可解决问题. 试题解析:(1)根据题意,得:y=50﹣x,(0≤x≤5...查看答案和解析>>
科目:初中数学 来源:安徽省2017-2018学年九年级上学期期末试卷数学 题型:填空题
已知一包糖果共有5种颜色(糖果只有颜色差别),如图是这包糖果分布百分比的统计图,在这包糖果中任意取一粒,则取出糖果的颜色为绿色或棕色的概率是_________.
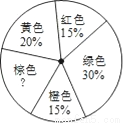
查看答案和解析>>
科目:初中数学 来源:安徽省2017-2018学年九年级上学期期末试卷数学 题型:单选题
如图,P是⊙O外一动点,PA、PB、CD是⊙O的三条切线,C、D分别在PA、PB上,连接OC、OD.设∠P为x°,∠COD为y°,则y随x的函数关系图象为( )
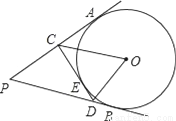
A. 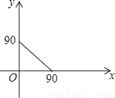 B.
B. 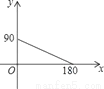
C. 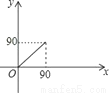 D.
D. 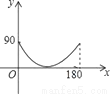
查看答案和解析>>
科目:初中数学 来源:山东省泰安市宁阳县2017-2018学年九年级上学期期末质量检测数学试卷 题型:填空题
在平面直角坐标系中,点C、D的坐标分别为C(2,3)、D(1,0),现以原点为位似中心,将线段CD放大得到线段AB.若点D的对应点B在x轴上且OB=2,则点C的对应点A的坐标为______________________________.
(4,6)或(﹣4,﹣6). 【解析】已知点D(1,0),点D的对应点B在x轴上,且OB=2,所以位似比为2,即可得点A的坐标为(2×2,3×2)或[2×(-2),3×(-2)],即点A的坐标为(4,6)或(-4,-6).查看答案和解析>>
科目:初中数学 来源:江苏省扬州市邗江区2017-2018学年八年级上学期期末考试数学试卷 题型:解答题
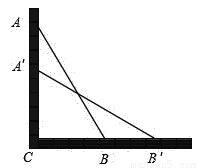
如图,一架长2.5m的梯子AB斜靠在墙AC上,∠C=90°,此时,梯子的底端B离墙底C的距离BC为0.7m.
(1)求此时梯子的顶端A距地面的高度AC;
(2)如果梯子的顶端A下滑了0.9m,那么梯子的顶端B在水平方向上向右滑动了多远?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com