
有40个数据,其中最大值为35,最小值为14,若取组距为4,则应该分的组数是( )
A. 4 B. 5 C. 6 D. 7
C 【解析】∵最大值为35,最小值为14, ∴在样本数据中最大值与最小值的差为35-14=21, 又∵组距为4, ∴应该分的组数=21÷4=5.25, ∴应该分成6组, 故选C.科目:初中数学 来源:人教版八年级下册数学全册综合测试卷 题型:单选题
若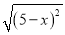 =x﹣5,则x的取值范围是( )
=x﹣5,则x的取值范围是( )
A. x<5 B. x≤5 C. x≥5 D. x>5
C 【解析】分析:本题考查的是 的运用. 解析:∵=x﹣5,∴ 故选C.查看答案和解析>>
科目:初中数学 来源:人教版七年级下册 第1-3章 综合测试卷 题型:填空题
如果两条直线和第三条直线________,那么这两条直线平行;若a∥b , b∥c,则________.
平行 a∥c 【解析】【解析】 如果两条直线和第三条直线平行,那么这两条直线平行; 若a∥b,b∥c,则a∥c. 故答案为:平行,a∥c.查看答案和解析>>
科目:初中数学 来源:北师大版八年级下册数学全册综合测试卷 题型:解答题
如图,在△ABC中,CA=CB,点D在BC上,且AB=AD=DC,求∠C的度数.
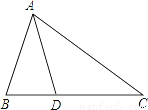
查看答案和解析>>
科目:初中数学 来源:北师大版八年级下册数学全册综合测试卷 题型:填空题
分解因式:x2y﹣4y= .
【解析】试题分析:先提取公因式y,然后再利用平方差公式进行二次分解. 【解析】 x2y﹣4y, =y(x2﹣4), =y(x+2)(x﹣2). 故答案为:y(x+2)(x﹣2).查看答案和解析>>
科目:初中数学 来源:北师大版八年级下册数学全册综合测试卷 题型:单选题
如图,在平行四边形ABCD中,过点C的直线CE⊥AB,垂足为E,若∠EAD=54°,则∠BCE的度数为( )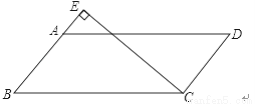
A. 54° B. 36° C. 46° D. 126°
B 【解析】∵四边形ABCD是平行四边形, ∴AD∥BC, ∵∠EAD=54°, ∴∠B=∠EAD=54°, ∵CE⊥AB, ∴∠BCE=90°-54°=36°. 故选B.查看答案和解析>>
科目:初中数学 来源:北师大版八年级下册数学全册综合测试卷 题型:单选题
若分式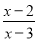 有意义,则
有意义,则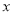 满足的条件是( )
满足的条件是( )
A. 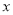 ≠0 B.
≠0 B. 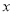 ≠2 C.
≠2 C. 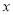 ≠3 D.
≠3 D. 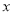 ≥3
≥3
查看答案和解析>>
科目:初中数学 来源:广东省2017-2018学年度九年级(上)数学第一次月考试卷(11月份)(解析版) 题型:解答题
已知:如图,AB⊥BD,CD⊥BD,垂足分别为B、D,AD和BC相交于点E,EF⊥BD,垂足为F,我们可以证明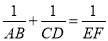 成立(不要求考生证明).
成立(不要求考生证明).
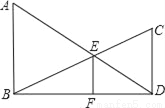
若将图中的垂线改为斜交,如图,AB∥CD,AD,BC相交于点E,过点E作EF∥AB交BD于点F,则:
(1)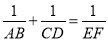 还成立吗?如果成立,请给出证明;如果不成立,请说明理由;
还成立吗?如果成立,请给出证明;如果不成立,请说明理由;
(2)请找出S△ABD,S△BED和S△BDC间的关系式,并给出证明.
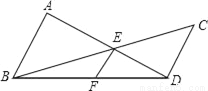
查看答案和解析>>
科目:初中数学 来源:2018届九年级中考数学专题复习同步练习题:平行四边形 题型:单选题
在?ABCD中,已知AB=(x+1)cm,BC=(x-2)cm,CD=4cm,则?ABCD的周长为( )
A. 5cm B. 10cm C. 14cm D. 28cm
B 【解析】∵四边形ABCD为平行四边形, ∴AB=CD, 即:x+1=4, 解得:x=3, ∴BC=x-2=1cm, ∴平行四边形ABCD的周长为:2×(1+4)=10cm. 故选:B.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com