
下列方程中有实数根的是( )
A. x2+2x+2=0 B. x2﹣2x+3=0 C. x2﹣3x+1=0 D. x2+3x+4=0
C 【解析】解:A.△=22﹣4×1×2=﹣6<0,则该方程无实数根,故本选项错误; B.△=(﹣2)2﹣4×1×3=﹣8<0,则该方程无实数根,故本选项错误; C.△=(﹣3)2﹣4×1×1=5>0,则该方程有实数根,故本选项正确; D.△=32﹣4×1×4=﹣7<0,则该方程无实数根,故本选项错误; 故选C.科目:初中数学 来源:2017年湖南省郴州市资兴市兴华实验学校中考数学模拟试卷 题型:解答题
解不等式组:  ,并把解集在数轴上表示出来.
,并把解集在数轴上表示出来.
查看答案和解析>>
科目:初中数学 来源:辽宁省抚顺县2017-2018学年八年级上学期期末教学质量检测数学试卷 题型:单选题
下列计算正确的是( )
A. 2a+3b=5ab B. 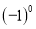 =l C.
=l C. 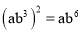 D.
D. 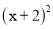
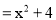
查看答案和解析>>
科目:初中数学 来源:江苏省扬州市邗江区2018届九年级(上)期中数学试卷 题型:填空题
在今年“全国助残日”捐款活动中,某班级第一小组7名同学积极捐出自己的零花钱,奉献自己的爱心.他们捐款的数额分别是(单位:元)50,20,50,30,25,55,25,这组数据的众数_____.
50和25 【解析】【解析】 50、25出现了2次,出现的次数最多,则众数是50和25,故答案为:50和25.查看答案和解析>>
科目:初中数学 来源:江苏省扬州市邗江区2018届九年级(上)期中数学试卷 题型:单选题
直线l与半径为r的⊙O相交,且点O到直线l的距离为6,则r的取值范围是( )
A. r<6 B. r=6 C. r>6 D. r≥6
C 【解析】【解析】 ∵直线l与半径为r的⊙O相交,且点O到直线l的距离d=6,∴r>6.故选C.查看答案和解析>>
科目:初中数学 来源:2017年江苏省扬州市中考数学模拟试卷(二) 题型:解答题
已知关于x的一元二次方程ax2+x﹣a=0(a≠0).
(1)求证:对于任意非零实数a,该方程恒有两个异号的实数根;
(2)设x1、x2是该方程的两个根,若|x1|+|x2|=4,求a的值.
(1)证明见解析(2)a=± 【解析】试题分析:(1)求证对于任意非零实数a,该方程恒有两个异号的实数根,即证明一元二次方程的根的判别式△=b2-4ac>0,则方程有两个不相等的实数根,若两根之积小于0,则方程有两个异号的实数根; (2)根据一元二次方程的根与系数的关系得到,两根之和与两根之积,把|x1|+|x2|=4变形成与两根之和与两根之积有关的式子,代入两根之和与两根之积,求得a...查看答案和解析>>
科目:初中数学 来源:2017年江苏省扬州市中考数学模拟试卷(二) 题型:填空题
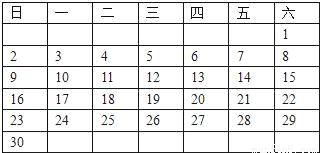
如图是2003年11月份的日历,现用一矩形在日历中任意框出4个数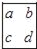 ,请用一个等式表示,a、b、c、d之间的关系_____.
,请用一个等式表示,a、b、c、d之间的关系_____.
查看答案和解析>>
科目:初中数学 来源:2017年湖北省中考数学模拟试卷 题型:解答题
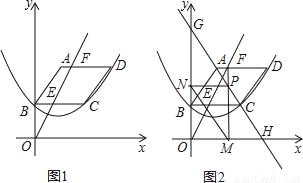
如图1,已知平行四边形ABCD顶点A的坐标为(2,6),点B在y轴上,且AD∥BC∥x轴,过B,C,D三点的抛物线y=ax2+bx+c(a≠0)的顶点坐标为(2,2),点F(m,6)是线段AD上一动点,直线OF交BC于点E.
(1)求抛物线的表达式;
(2)设四边形ABEF的面积为S,请求出S与m的函数关系式,并写出自变量m的取值范围;
(3)如图2,过点F作FM⊥x轴,垂足为M,交直线AC于P,过点P作PN⊥y轴,垂足为N,连接MN,直线AC分别交x轴,y轴于点H,G,试求线段MN的最小值,并直接写出此时m的值.
(1)抛物线解析式为y=x2﹣x+3;(2)S=m﹣3(2<m≤6);(3)当m=时,MN最小=. 【解析】试题分析:(1)根据平行四边形的性质和抛物线的特点确定出点D,然而用待定系数法确定出抛物线的解析式.(2)根据AD∥BC∥x轴,且AD,BC间的距离为3,BC,x轴的距离也为3,F(m,6),确定出E(,3),从而求出梯形的面积.(3)先求出直线AC解析式,然后根据FM⊥x轴,表示出点...查看答案和解析>>
科目:初中数学 来源:河北省2017-2018学年九年级第一学期第一次月考数学试卷 题型:解答题
已知关于x的一元二次方程x2﹣2mx+(m﹣1)2=0有两个实数根x1,x2.
(1)求m的取值范围;
(2)当x12+x22=28时,求m的值.
(1)m≥;(2)符合条件的m的值为3. 【解析】试题分析:(1)若一元二次方程有两个等实数根,则根的判别式△=b2-4ac≥0,建立关于m的不等式,即可求出m的取值范围; (2)根据根与系数的关系,可得x1+x2=2m,x1·x2=(m﹣1)2,再根据x12+x22=(x1+x2)2-2x1·x2即可求得m的值,结合(1)即可确定出m的具体值. 试题解析:(1)∵原方程有两个实...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com