
如果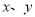 为实数,且
为实数,且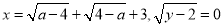 ,则
,则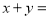 _____ .
_____ .
科目:初中数学 来源:山东省诸城市2017-2018学年七年级上学期第二次月考数学试卷 题型:单选题
如图所示,边长为a的正方形中阴影部分的面积为( )
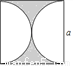
A. a2﹣π(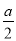 )2 B. a2﹣πa2 C. a2﹣πa D. a 2﹣2πa
)2 B. a2﹣πa2 C. a2﹣πa D. a 2﹣2πa
查看答案和解析>>
科目:初中数学 来源:2016-2017学年陕西师大附中七年级(下)第一次月考数学试卷 题型:填空题
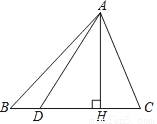
如图,AH⊥BC交BC于H,那么以AH为高的三角形有_____个.
查看答案和解析>>
科目:初中数学 来源:四川省遂宁市黄泥学校2016-2017学年上期八年级期中测评数学试卷 题型:解答题
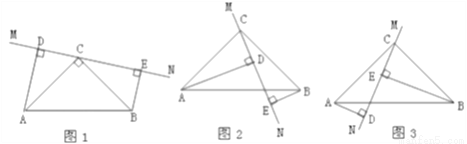
在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.
(1)当直线MN绕点C旋转到图1的位置时,求证:DE=AD+BE;
(2)当直线MN绕点C旋转到图2的位置时,求证:DE=AD-BE;
(3)当直线MN绕点C旋转到图3的位置时,试问DE、AD、BE具有怎样的等量关系?请直接写出这个等量关系.
查看答案和解析>>
科目:初中数学 来源:四川省遂宁市黄泥学校2016-2017学年上期八年级期中测评数学试卷 题型:解答题
计算:(1)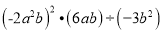 (2)
(2)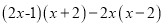
(3)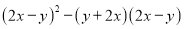 (4)
(4)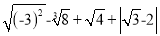
查看答案和解析>>
科目:初中数学 来源:四川省遂宁市黄泥学校2016-2017学年上期八年级期中测评数学试卷 题型:单选题
如图,AD是△ABC的中线,E,F分别是AD和AD延长线上的点,且DE=DF,连结BF,CE.下列说法:①△ABD和△ACD面积相等;②∠BAD=∠CAD;③△BDF≌△CDE;④BF∥CE;⑤CE=AE.其中正确的有( )
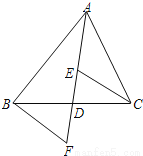
A. 1个 B. 2个 C. 3个 D. 4个
C 【解析】试题分析:①∵AD是△ABC的中线,∴BD=CDF,∴△ABD和△ACD面积相等;故①正确; ②若在△ABC中,当AB≠AC时,AD不是∠BAC的平分线,即∠BAD≠∠CAD.即②不一定正确; ③∵AD是△ABC的中线,∴BD=CD, 在△BDF和△CDE中,∵BD=CD,∠BDF=∠CDE,DF=DE,∴△BDF≌△CDE(SAS).故③正确; ④∵△B...查看答案和解析>>
科目:初中数学 来源:四川省遂宁市黄泥学校2016-2017学年上期八年级期中测评数学试卷 题型:单选题
如(x+m)与(x+3)的乘积中不含x的一次项,则m的值为 ( )
A. –3 B. 3 C. 0 D. 1
A 【解析】(x+m)(x+3)=x2+(3+m)x+3m, 因为结果不含x的一次项,所以3+m=0,m=-3, 故选A.查看答案和解析>>
科目:初中数学 来源:重庆市江津区2016-2017学年八年级下学期期末考试数学试卷 题型:填空题
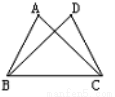
如图,∠ABC=∠DCB,请补充一个条件: ,使△ABC≌△DCB.
查看答案和解析>>
科目:初中数学 来源:2017年广东省河源市中考数学一诊试卷 题型:解答题
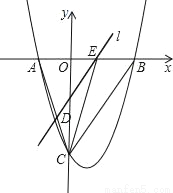
如图,抛物线y=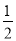 x2﹣
x2﹣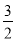 x﹣9与x轴交于A、B两点,与y轴交于点C,连接BC、AC.
x﹣9与x轴交于A、B两点,与y轴交于点C,连接BC、AC.
(1)求AB和OC的长;
(2)点E从点A出发,沿x轴向点B运动(点E与点A、B不重合),过点E作直线l平行BC,交AC于点D.设AE的长为m,△ADE的面积为s,求s关于m的函数关系式,并写出自变量m的取值范围;
(3)在(2)的条件下,连接CE,求△CDE面积的最大值;此时,求出以点E为圆心,与BC相切的圆的面积(结果保留π).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com