
若分式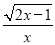 有意义,则x的取值范围是( )
有意义,则x的取值范围是( )
A. x≤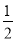 B. x≤
B. x≤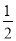 且x≠0 C. x≥
且x≠0 C. x≥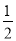 D. x>
D. x>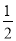 且x≠0
且x≠0
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:初中数学 来源:甘肃省定西市安定区2017-2018学年九年级上学期期末考试数学试卷 题型:解答题
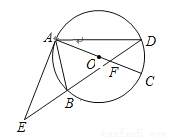
如图,⊙O的直径AC与弦BD相交于点F,点E是DB延长线上一点,∠EAB=∠ADB.
(1)求证:EA是⊙O的切线;
(2)已知点B是EF的中点,AF=4,CF=2,求AE的长.
查看答案和解析>>
科目:初中数学 来源:江苏省东台市第三教育联盟2017-2018学年度第一学期第三次阶段检测七年级数学试卷 题型:填空题
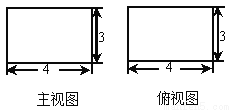
长方体的主视图与俯视图如图所示,则这个长方体的体积是________.
查看答案和解析>>
科目:初中数学 来源:2017年贵州省中考数学二模试卷 题型:解答题
我省某地区为了了解2016年初中毕业生毕业去向,对部分九年级学生进行了抽样调查,就九年级学生毕业后的四种去向:A.读普通高中;B.读职业高中;C.直接进入社会就业;D.其他(如出国等)进行数据统计,并绘制了两幅不完整的统计图(如图1,如图2)
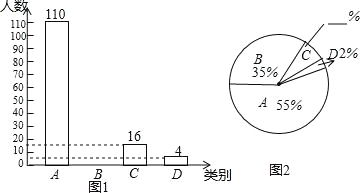
(1)填空:该地区共调查了 名九年级学生;
(2)将两幅统计图中不完整的部分补充完整;
(3)若该地区2016年初中毕业生共有3500人,请估计该地区今年初中毕业生中读普通高中的学生人数;
(4)老师想从甲,乙,丙,丁4位同学中随机选择两位同学了解他们毕业后的去向情况,请用画树状图或列表的方法求选中甲同学的概率.
(1)200;(2)详见解析;(3)1925;(4). 【解析】 试题分析:(1)根据统计图可以得到本次调查的九年级学生数;(2)根据题目中的数据可以得到统计图中未知的数据,从而可以解答本题;(3)根据统计图中的数据可以估计该地区今年初中毕业生中读普通高中的学生人数;(4)根据题意可以画出相应的树状图,从而可以求得选中甲同学的概率. 试题解析:(1)该地区调查的九年级学生数为:1...查看答案和解析>>
科目:初中数学 来源:2017年贵州省中考数学二模试卷 题型:填空题
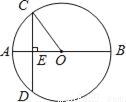
如图,AB为圆O的直径,弦CD⊥AB,垂足为点E,连接OC,若OC=5,CD=8,则AE=_____.
查看答案和解析>>
科目:初中数学 来源:2017年贵州省中考数学二模试卷 题型:单选题
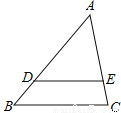
如图,在△ABC中,点D、E分AB、AC边上,DE∥BC,若AD:AB=3:4,AE=6,则AC等于( )
A.3 B.4 C.6 D.8
D 【解析】 首先由DE∥BC可以得到AD:AB=AE:AC,而AD:AB=3:4,AE=6,由此即可求出AC. 【解析】 ∵DE∥BC, ∴△ADE∽△ABC, ∴AD:AB=AE:AC, 而AD:AB=3:4,AE=6, ∴3:4=6:AC, ∴AC=8. 故选D.查看答案和解析>>
科目:初中数学 来源:黄金30题系列 九年级数学 大题易丢分 题型:解答题
某商家经销一种绿茶,用于装修门面已投资3000元.已知绿茶每千克成本50元,经研究发现销量y(kg)随销售单价x(元/ kg)的变化而变化,具体变化规律如下表所示:

设该绿茶的月销售利润为w(元)(销售利润=单价×销售量-成本)
(1)请根据上表,求出y与x之间的函数关系式(不必写出自变量x的取值范围);
(2)求w与x之间的函数关系式(不必写出自变量x的取值范围),并求出x为何值时,w的值最大?
(3)若在第一个月里,按使w获得最大值的销售单价进行销售后,在第二个月里受物价部门干预,销售单价不得高于80元,要想在全部收回装修投资的基础上使第二个月的利润至少达到1700元,那么第二个月时里应该确定销售单价在什么范围内?
【答案】(1)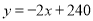 ;
;
(2)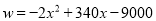 ,当
,当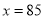 时,
时, 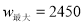 ;
;
(3)当销售单价为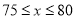 元时,在全部收回投资的基础上使第二个月的利润不低于1700元.
元时,在全部收回投资的基础上使第二个月的利润不低于1700元.
【解析】【试题分析】(1)根据表格的数据.易得销售单价每升高5元,销售量下降10Kg,即w是x的一次函数,故设设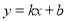 ,将(70,100),(75,90)代入上式得:
,将(70,100),(75,90)代入上式得:
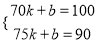 解得:
解得: 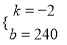 ,则
,则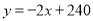 ;
;
(2)销售利润=单位质量的利润乘以销售量,即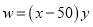
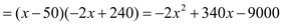 ,化为顶点式得,
,化为顶点式得, 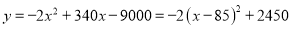 ,当
,当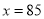 时,
时, 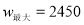
(3)由(2)知,第1个月还有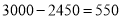 元的投资成本没有收回.则要想在全部收投资的基础上使第二个月的利润达到1700元, 即
元的投资成本没有收回.则要想在全部收投资的基础上使第二个月的利润达到1700元, 即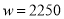 才可以,可得方程
才可以,可得方程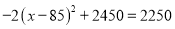 ,解得:
,解得: 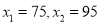 根据题意
根据题意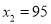 不合题意,应舍去.当
不合题意,应舍去.当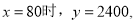 ,因为-2<0,则抛物线开口向下,当
,因为-2<0,则抛物线开口向下,当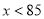 时,
时, 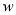 随
随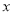 的增大而增大,当
的增大而增大,当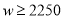 ,且销售单价不高于80时,
,且销售单价不高于80时, 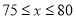
【试题解析】
(1)设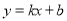 ,将(70,100),(75,90)代入上式得:
,将(70,100),(75,90)代入上式得:
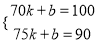 解得:
解得: 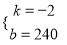 ,则
,则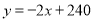 ,
,
将表中其它对应值代入上式均成立,所以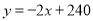
(2)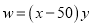
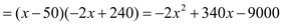
因此, 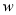 与
与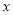 的关系式为
的关系式为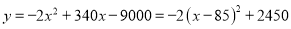
当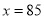 时,
时, 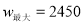
(3)由(2)知,第1个月还有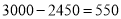 元的投资成本没有收回.
元的投资成本没有收回.
则要想在全部收投资的基础上使第二个月的利润达到1700元, 即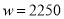 才可以,
才可以,
可得方程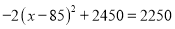 ,解得:
,解得: 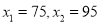
根据题意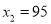 不合题意,应舍去.当
不合题意,应舍去.当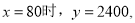 ,
,
∵-2<0,∴,当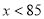 时,
时, 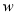 随
随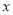 的增大而增大,
的增大而增大,
当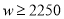 ,且销售单价不高于80时,
,且销售单价不高于80时, 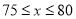
答:当销售单价为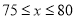 元时,在全部收回投资的基础上使第二个月的利润不低于1700元
元时,在全部收回投资的基础上使第二个月的利润不低于1700元
【题型】解答题
【结束】
18
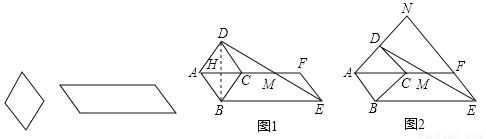
如图,分别是可活动的菱形和平行四边形学具,已知平行四边形较短的边与菱形的边长相等.
(1)在一次数学活动中,某小组学生将菱形的一边与平行四边形较短边重合,摆拼成如图1所示的图形,AF经过点C,连接DE交AF于点M,观察发现:点M是DE的中点.
下面是两位学生有代表性的证明思路:
思路1:不需作辅助线,直接证三角形全等;
思路2:不证三角形全等,连接BD交AF于点H.…
请参考上面的思路,证明点M是DE的中点(只需用一种方法证明);
(2)如图2,在(1)的前提下,当∠ABE=135°时,延长AD、EF交于点N,求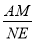 的值;
的值;
(3)在(2)的条件下,若 =k(k为大于
=k(k为大于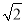 的常数),直接用含k的代数式表示
的常数),直接用含k的代数式表示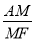 的值.
的值.
查看答案和解析>>
科目:初中数学 来源:黄金30题系列 九年级数学 大题易丢分 题型:解答题
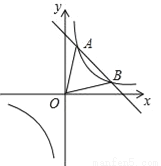
如图,一次函数y=kx+b与反比例函数y= 的图象交于A(1,6),B(3,n)两点.
的图象交于A(1,6),B(3,n)两点.
(1)求反比例函数和一次函数的表达式;
(2)根据图象写出不等式kx+b﹣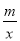 >0的解集;
>0的解集;
(3)若点M在x轴上、点N在y轴上,且以M、N、A、B为顶点的四边形是平行四边形,请直接写出点M、N的坐标.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题八年级人教版数学试卷(A卷) 题型:填空题
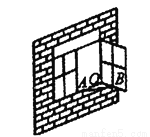
如图,一扇窗户打开后,用窗钩AB可将其固定,这里所运用的几何原理是______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com