
某商家经销一种绿茶,用于装修门面已投资3000元.已知绿茶每千克成本50元,经研究发现销量y(kg)随销售单价x(元/ kg)的变化而变化,具体变化规律如下表所示:

设该绿茶的月销售利润为w(元)(销售利润=单价×销售量-成本)
(1)请根据上表,求出y与x之间的函数关系式(不必写出自变量x的取值范围);
(2)求w与x之间的函数关系式(不必写出自变量x的取值范围),并求出x为何值时,w的值最大?
(3)若在第一个月里,按使w获得最大值的销售单价进行销售后,在第二个月里受物价部门干预,销售单价不得高于80元,要想在全部收回装修投资的基础上使第二个月的利润至少达到1700元,那么第二个月时里应该确定销售单价在什么范围内?
【答案】(1)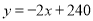 ;
;
(2)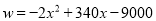 ,当
,当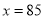 时,
时, 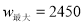 ;
;
(3)当销售单价为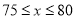 元时,在全部收回投资的基础上使第二个月的利润不低于1700元.
元时,在全部收回投资的基础上使第二个月的利润不低于1700元.
【解析】【试题分析】(1)根据表格的数据.易得销售单价每升高5元,销售量下降10Kg,即w是x的一次函数,故设设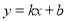 ,将(70,100),(75,90)代入上式得:
,将(70,100),(75,90)代入上式得:
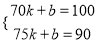 解得:
解得: 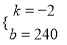 ,则
,则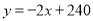 ;
;
(2)销售利润=单位质量的利润乘以销售量,即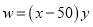
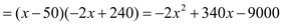 ,化为顶点式得,
,化为顶点式得, 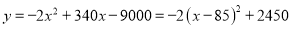 ,当
,当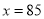 时,
时, 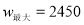
(3)由(2)知,第1个月还有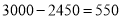 元的投资成本没有收回.则要想在全部收投资的基础上使第二个月的利润达到1700元, 即
元的投资成本没有收回.则要想在全部收投资的基础上使第二个月的利润达到1700元, 即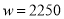 才可以,可得方程
才可以,可得方程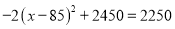 ,解得:
,解得: 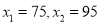 根据题意
根据题意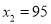 不合题意,应舍去.当
不合题意,应舍去.当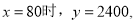 ,因为-2<0,则抛物线开口向下,当
,因为-2<0,则抛物线开口向下,当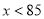 时,
时, 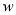 随
随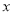 的增大而增大,当
的增大而增大,当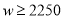 ,且销售单价不高于80时,
,且销售单价不高于80时, 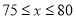
【试题解析】
(1)设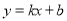 ,将(70,100),(75,90)代入上式得:
,将(70,100),(75,90)代入上式得:
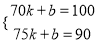 解得:
解得: 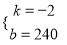 ,则
,则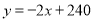 ,
,
将表中其它对应值代入上式均成立,所以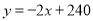
(2)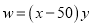
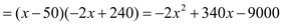
因此, 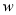 与
与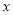 的关系式为
的关系式为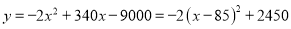
当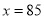 时,
时, 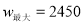
(3)由(2)知,第1个月还有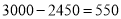 元的投资成本没有收回.
元的投资成本没有收回.
则要想在全部收投资的基础上使第二个月的利润达到1700元, 即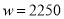 才可以,
才可以,
可得方程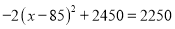 ,解得:
,解得: 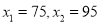
根据题意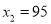 不合题意,应舍去.当
不合题意,应舍去.当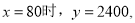 ,
,
∵-2<0,∴,当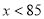 时,
时, 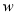 随
随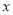 的增大而增大,
的增大而增大,
当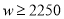 ,且销售单价不高于80时,
,且销售单价不高于80时, 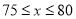
答:当销售单价为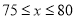 元时,在全部收回投资的基础上使第二个月的利润不低于1700元
元时,在全部收回投资的基础上使第二个月的利润不低于1700元
【题型】解答题
【结束】
18
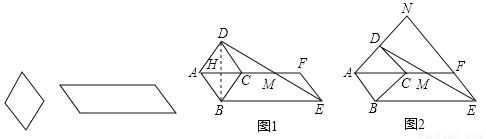
如图,分别是可活动的菱形和平行四边形学具,已知平行四边形较短的边与菱形的边长相等.
(1)在一次数学活动中,某小组学生将菱形的一边与平行四边形较短边重合,摆拼成如图1所示的图形,AF经过点C,连接DE交AF于点M,观察发现:点M是DE的中点.
下面是两位学生有代表性的证明思路:
思路1:不需作辅助线,直接证三角形全等;
思路2:不证三角形全等,连接BD交AF于点H.…
请参考上面的思路,证明点M是DE的中点(只需用一种方法证明);
(2)如图2,在(1)的前提下,当∠ABE=135°时,延长AD、EF交于点N,求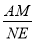 的值;
的值;
(3)在(2)的条件下,若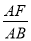 =k(k为大于
=k(k为大于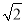 的常数),直接用含k的代数式表示
的常数),直接用含k的代数式表示 的值.
的值.
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:甘肃省定西市安定区2017-2018学年九年级上学期期末考试数学试卷 题型:填空题
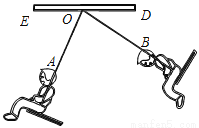
如图所示,小明坐在秋千上,秋千旋转了80°,∠AOE=60°,则∠DOB=_______.
查看答案和解析>>
科目:初中数学 来源:江苏省东台市第三教育联盟2017-2018学年度第一学期第三次阶段检测七年级数学试卷 题型:单选题
下列计算正确的是( )
A. 3a+4b=7ab B. 7a-3a=4 C. 3a+a=3a2 D. 3a2b-4a2b=-a2b
D 【解析】A.3a+4b不能合并,所以3a+4b=7ab错误; B. 7a-3a=4a,故原选项错误; C. 3a+a=4a,故原选项错误; D. 3a2b-4a2b=-a2b 正确. 故选D.查看答案和解析>>
科目:初中数学 来源:2017年贵州省中考数学二模试卷 题型:单选题
若分式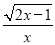 有意义,则x的取值范围是( )
有意义,则x的取值范围是( )
A. x≤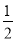 B. x≤
B. x≤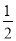 且x≠0 C. x≥
且x≠0 C. x≥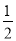 D. x>
D. x>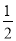 且x≠0
且x≠0
查看答案和解析>>
科目:初中数学 来源:2017年贵州省中考数学二模试卷 题型:单选题
一组数据2、5、4、3、5、4、5的中位数和众数分别是( ).
A.3.5,5 B.4,4 C.4,5 D.4.5,4
C. 【解析】 试题分析:根据众数和中位数的概念求解.这组数据按照从小到大的顺序排列为:2,3,4,4,5,5,5,则众数为5,中位数为4. 故选:C.查看答案和解析>>
科目:初中数学 来源:黄金30题系列 九年级数学 大题易丢分 题型:解答题
已知关于x的一元二次方程x2-(2k+1)x+k2+2k=0有两个实数根x1,x2.
(1)求实数k的取值范围;
(2)是否存在实数k,使得x1·x2-x12-x22≥0成立?若存在,请求出k的值;若不存在,请说明理由.
【答案】(1)当k≤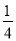 时,原方程有两个实数根(2)不存在实数k,使得x1·x2-x12-x22≥0成立
时,原方程有两个实数根(2)不存在实数k,使得x1·x2-x12-x22≥0成立
【解析】试题分析:(1)根据一元二次方程根的判别式列出不等式,解之即可;(2)本题利用韦达定理解决.
试题解析:
(1)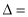
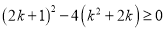 ,解得
,解得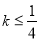
(2)由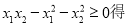
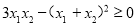 ,
,
由根与系数的关系可得: 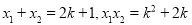
代入得: 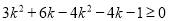 ,
,
化简得: 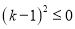 ,
,
得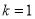 .
.
由于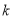 的取值范围为
的取值范围为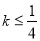 ,
,
故不存在k使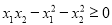 。
。
【题型】解答题
【结束】
13
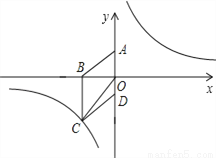
如图,在平面直角坐标系中,已知四边形ABCD为菱形,且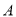 (0,3)、
(0,3)、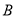 (﹣4,0).
(﹣4,0).
(1)求经过点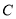 的反比例函数的解析式;
的反比例函数的解析式;
(2)设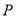 是(1)中所求函数图象上一点,以
是(1)中所求函数图象上一点,以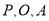 顶点的三角形的面积与△COD的面积相等.求点P的坐标.
顶点的三角形的面积与△COD的面积相等.求点P的坐标.
查看答案和解析>>
科目:初中数学 来源:黄金30题系列 九年级数学 大题易丢分 题型:解答题
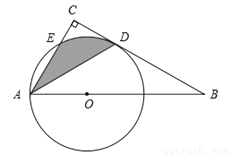
如图,Rt△ABC中,∠BAC=60°,点O为Rt△ABC斜边AB上的一点,以OA为半径的⊙O与BC切于点D,与AC交于点E,连接AD.
(1)求∠CAD的度数;
(2)若OA = 2,求阴影部分的面积(结果保留π).
【答案】(1)∠CAD的度数为30°;
(2)阴影部分的面积为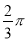 .
.
【解析】试题分析:(1)连接OD.由切线的性质可知OD⊥BC,从而可证明AC∥OD,由平行线的性质和等腰三角形的性质可证明∠CAD=∠OAD;(2)连接OE,ED、OD.先证明ED∥AO,然后依据同底等高的两个三角形的面积相等可知S△AED=S△EDO,于是将阴影部分的面积可转化为扇形EOD的面积求解即可.
试题解析:(1)连接OD,
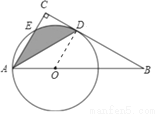
∵BC是⊙O的切线,D为切点,
∴OD⊥BC.
又∵AC⊥BC,
∴OD∥AC,
∴∠ADO=∠CAD.
又∵OD=OA,
∴∠ADO=∠OAD,
∴∠CAD=∠OAD=30°.
(2)连接OE,ED.
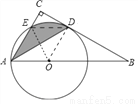
∵∠BAC=60°,OE=OA,
∴△OAE为等边三角形,
∴∠AOE=60°,
∴∠ADE=30°.
又∵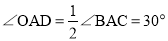 ,
,
∴∠ADE=∠OAD,
∴ED∥AO,
∴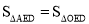
∴阴影部分的面积 = 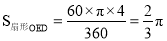 .
.
【题型】解答题
【结束】
6
如图是由两个长方体组合而成的一个立体图形的三视图,根据图中所标尺寸(单位:mm),求这个立体图形的表面积.
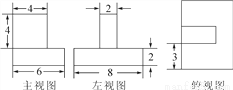
查看答案和解析>>
科目:初中数学 来源:黄金30题系列 七年级数学 小题易丢分 题型:填空题
若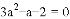 ,则
,则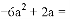 ____________
____________
查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题八年级人教版数学试卷(A卷) 题型:单选题
已知△ABC的六个元素,下面甲、乙、丙三个三角形中标出了某些元素,则与△ABC全等的三角形是( )
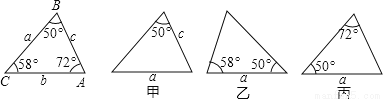
A. 只有乙 B. 只有丙 C. 甲和乙 D. 乙和丙
D 【解析】乙满足ASA,丙满足AAS,所以选D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com