
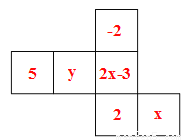
如图是一个正方体的表面展开图,若正方体中相对的面上的数互为相反数,则2x-y的值为_________.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:新疆乌鲁木齐市2018届九年级上学期期末考试数学试卷 题型:单选题
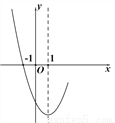
抛物线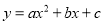 的部分图象如图所示(对称轴是
的部分图象如图所示(对称轴是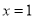 ),若
),若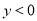 ,则
,则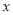 的取值范围是( )
的取值范围是( )
A. 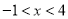 B.
B. 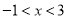 C.
C. 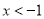 或
或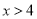 D.
D. 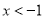 或
或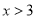
查看答案和解析>>
科目:初中数学 来源:江苏省盐城市盐都区2017届九年级上学期期末考试数学试卷 题型:填空题
在Rt△ABC中,∠C=90°,AC=6,BC=8,则△ABC的外接圆的半径是 .
5 【解析】分析:首先根据勾股定理,得其斜边是10,再根据直角三角形的外接圆的半径是斜边的一半,得其半径是5. 本题解析:∵∠C=90°,AC=6,BC=8, ∴BA=10, ∴其外接圆的半径为5.故答案为:5.查看答案和解析>>
科目:初中数学 来源:江苏省泰兴市2017-2018学年七年级上学期期末考试数学试卷 题型:解答题
直线AB、CD相交于点O,OE平分∠BOD,OF⊥CD,垂足为O.
(1)若∠EOF=54°,求∠AOC的度数;
(2)①在∠AOD的内部作射线OG⊥OE;
②试探索∠AOG与∠EOF之间有怎样的关系?并说明理由.
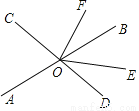
查看答案和解析>>
科目:初中数学 来源:江苏省泰兴市2017-2018学年七年级上学期期末考试数学试卷 题型:解答题
解方程
(1) 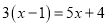 (2)
(2) 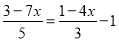
查看答案和解析>>
科目:初中数学 来源:江苏省泰兴市2017-2018学年七年级上学期期末考试数学试卷 题型:填空题
如图,∠1=25°,则射线OA表示为南偏东________.
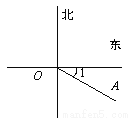
查看答案和解析>>
科目:初中数学 来源:河南省2017-2018学年八年级上学期期末考试数学试卷 题型:解答题
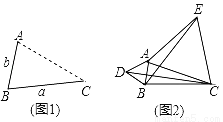
(1)发现:如图1,点A为线段BC外一动点,且BC=a,AB=b.
①填空:当点A位于 时,线段AC的长取得最大值,且最大值为 (用含a,b的式子表示)
(2)应用:点A为线段BC外一动点,且BC=3,AB=1,如图2所示,分别以AB、AC为边,作等边三角形ABD和等边三角形ACE,连接CD,BE.
①请找出图中与BE相等的线段,并说明理由;
②直接写出线段BE长的最大值.
查看答案和解析>>
科目:初中数学 来源:河南省2017-2018学年八年级上学期期末考试数学试卷 题型:单选题
如图,在∠AOB的两边上,分别取OM=ON,再分别过点M、N作OA、OB的垂线,交点为P,画射线OP,则OP平分∠AOB的依据是( )
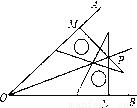
A. SAS B. SSS C. AAS D. HL
D 【解析】试题解析:在Rt△OMP和Rt△ONP中, , ∴Rt△OMP≌Rt△ONP(HL), ∴∠MOP=∠NOP, ∴OP是∠AOB的平分线. 故选D.查看答案和解析>>
科目:初中数学 来源:北京市密云区2017-2018学年度第一学期期末考试初三数学试卷 题型:填空题
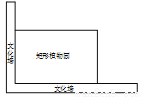
学校组织“美丽校园我设计”活动.某同学打算利用学校文化墙的墙角建一个矩形植物园.其中矩形植物园的两邻边之和为4m,设矩形的一边长为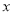 m,矩形的面积为
m,矩形的面积为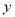 m2.则函数
m2.则函数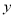 的表达式为______________,该矩形植物园的最大面积是_______________ m2.
的表达式为______________,该矩形植物园的最大面积是_______________ m2.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com