
一个口袋中有红球、白球共20只,这些球除颜色外都相同,将口袋中的球搅拌均匀,从中随机摸出一只球,记下它的颜色后再放回,不断重复这一过程,共摸了50次,发现有30次摸到红球,则估计这个口块中有红球大约多少只?( )
A.8只 B.12只 C.18只 D.30只
科目:初中数学 来源:江苏省苏州市2017-2018学年第二学期八年级期中数学模拟试卷 题型:解答题
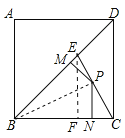
如图,E为正方形ABCD对角线BD上的一点,且BE=BC=1.

(1)求∠DCE的度数;
(2)点P在EC上,作PM⊥BD于M,PN⊥BC于N,求PM+PN的值.
【答案】(1)22.5°,(2)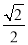 .
.
【解析】
试题分析:(1)由正方形的性质得到,∠BCD=90°,∠DBC=45°,推出AB=BE,根据三角形的内角和定理求出∠BCE=∠BEC=67.5°,根据∠DCE=∠DCB-∠BCE即可求出答案.
(2)连接BP,作EF⊥BC于F,则∠EFB=90°,得出△BEF是等腰直角三角形,从而求得BF=EF=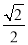 ,然后根据S△BPE+S△BPC=S△BEC,求得PM+PN=EF,即可求得.
,然后根据S△BPE+S△BPC=S△BEC,求得PM+PN=EF,即可求得.
试题解析:(1)在正方形ABCD中,∠BCD=90°,∠DBC=45°,
∵BE=BC,
∴AB=BE,
∴∠BCE=∠BEC=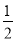 (180°-∠DBC)=67.5°,
(180°-∠DBC)=67.5°,
∴∠DCE=∠DCB-∠BCE=90°-67.5°=22.5°,
(2)连接BP,作EF⊥BC于F,则∠EFB=90°,
∵∠EBF=45°,
∴△BEF是等腰直角三角形,
∵BE=BC=1,
∴BF=EF=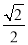 ,
,
∵PM⊥BD,PN⊥BC,
∴S△BPE+S△BPC=S△BEC,
即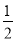 BE•PM+
BE•PM+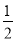 BC•PN=
BC•PN=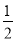 BC•EF,
BC•EF,
∵BE=BC,
∴PM+PN=EF=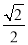 .
.
考点:1.正方形的性质;2.等腰直角三角形.
【题型】解答题
【结束】
28
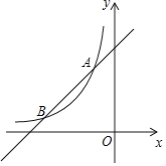
如图,一次函数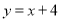 的图像与反比例函数
的图像与反比例函数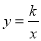 (
(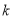 为常数,且
为常数,且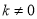 )的图像交于
)的图像交于
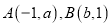 两点.
两点.
(1)求反比例函数的表达式;
(2)在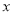 轴上找一点
轴上找一点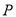 ,使
,使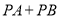 的值最小,求满足条件的点
的值最小,求满足条件的点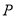 的坐标;
的坐标;
(3)在(2)的条件下求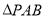 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源:江苏省2017-2018学年七年级下学期第一次月考数学试卷 题型:填空题
在等腰△ABC中,如果两边长分别为6cm、10cm,则这个等腰三角形的底边长为________.
查看答案和解析>>
科目:初中数学 来源:青岛版九年级下册数学 第6章事件的概率 单元检测 题型:填空题
不透明袋子中装有9个球,其中有2个红球、3个绿球和4个蓝球,这些球除颜色外无其他差别.从袋子中随机取出1个球,则它是红球的概率是 .
查看答案和解析>>
科目:初中数学 来源:青岛版九年级下册数学 第6章事件的概率 单元检测 题型:单选题
小明、小雪、丁丁和东东在公园玩飞行棋,四人轮流掷骰子,小明掷骰子7次就掷出了4次6,则小明掷到数字6的概率是( )
A.  B.
B.  C.
C.  D. 不能确定
D. 不能确定
查看答案和解析>>
科目:初中数学 来源:2017-2018学年河北省保定市莲池区九年级(上)期末数学试卷 题型:解答题
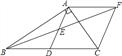
如图,在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.
(1)求证:△AEF≌△DEB;
(2)求证:四边形ADCF是菱形;
(3)若AC=4,AB=5,求菱形ADCF的面积.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年河北省保定市莲池区九年级(上)期末数学试卷 题型:单选题
菱形,矩形,正方形都具有的性质是( )
A. 四条边相等,四个角相等 B. 对角线相等
C. 对角线互相垂直 D. 对角线互相平分
查看答案和解析>>
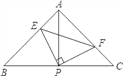
科目:初中数学 来源:山东省青岛市南区2016-2017学年八年级下学期期中阶段检测数学试卷 题型:单选题
已知
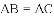
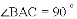 ,直角
,直角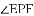
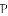
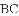
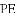
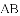
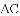
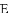
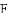
①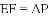
②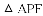
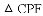
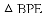
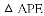
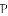
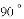 得到的;
得到的;
③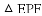
④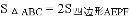 .
.
其中始终成立的有( )
A. 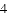
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com