
在下列条件中,能断定△ABC为等腰三角形的是( )
A. ∠A=30°,∠B=60° B. ∠A=50°,∠B=80°
C. AB=AC=2,BC=4 D. AB=3,BC=7,周长为18
B 【解析】A.根据三角形内角和定理得,∠C=180°﹣60°﹣30°=90°,故不是等腰三角形; B.根据三角形内角和定理得,∠C=180°﹣50°﹣80°=50°,故是等腰三角形; C.根据三角形中三边的关系知,任意两边之和大于第三边,而AB+AC=4=BC,不能构成三角形; D.周长为18,而AB+BC=10,故第三边为8,故不是等腰三角形, 故选B. 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:初中数学 来源:2017年贵州省中考数学二模试卷 题型:单选题
一组数据2、5、4、3、5、4、5的中位数和众数分别是( ).
A.3.5,5 B.4,4 C.4,5 D.4.5,4
C. 【解析】 试题分析:根据众数和中位数的概念求解.这组数据按照从小到大的顺序排列为:2,3,4,4,5,5,5,则众数为5,中位数为4. 故选:C.查看答案和解析>>
科目:初中数学 来源:黄金30题系列 七年级数学 小题易丢分 题型:单选题
如图所示,此正方体的展开图是图②中的( )
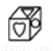
A. 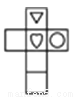 B.
B. 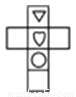 C.
C. 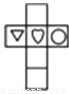 D.
D. 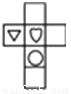
查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题八年级人教版数学试卷(A卷) 题型:解答题
先化简,再求值:
(1)2(x+1)(x﹣1)﹣x(2x﹣1),其中x=﹣2;
(2)[(x+y)(x﹣y)+2y(x﹣y)﹣(x﹣y)2]÷(2y),其中x=1,y=2.
(1)x-2;-4;(2)2x-2y,-2. 【解析】试题分析:(1)原式第一项利用平方差公式化简,第二项利用单项式乘以多项式,去括号合并后得到最简结果,将的值代入计算即可得到结果; (2)原式括号中第一项利用平方差公式化简,第二项利用单项式乘以多项式,第三项用完全平方公式,合并后利用多项式除以单项式法则计算得到最简结果,将与的值代入计算即可求出值. 试题解析: 原式 当时, ...查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题八年级人教版数学试卷(A卷) 题型:填空题
已知等腰三角形的一边等于3,一边等于6,那么它的周长等于_______________.
15 【解析】试题解析:①若腰长为3,底边长为6, ∵3+3=6, ∴不能组成三角形,舍去; ②若腰长为6,底边长为3, 则它的周长是:6+6+3=15. ∴它的周长是15, 故答案为:15.查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题八年级人教版数学试卷(A卷) 题型:单选题
已知△ABC的六个元素,下面甲、乙、丙三个三角形中标出了某些元素,则与△ABC全等的三角形是( )
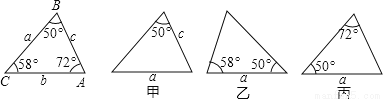
A. 只有乙 B. 只有丙 C. 甲和乙 D. 乙和丙
D 【解析】乙满足ASA,丙满足AAS,所以选D.查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题八年级北师大版数学试卷(B卷) 题型:解答题
如图,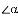
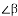
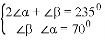 ,且CD∥EF,
,且CD∥EF,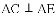
(1)求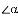
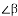
(2)判断AB与CD的位置关系,并说明理由;
(3)求∠C的度数。
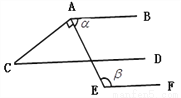
查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题八年级北师大版数学试卷(B卷) 题型:单选题
在平面直角坐标系中,点P(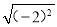 ,
, 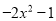 )所在的象限是( )
)所在的象限是( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
D 【解析】∵ , , ∴点P(, )在第四象限, 故选D.查看答案和解析>>
科目:初中数学 来源:黄金30题系列 八年级数学 大题好拿分 题型:解答题
分别画出下列各多边形的对角线,并观察图形完成下列问题:
(1)试写出用n边形的边数n表示对角线总条数S的式子: .
(2)从十五边形的一个顶点可以引出 条对角线,十五边形共有 条对角线:
(3)如果一个多边形对角线的条数与它的边数相等,求这个多边形的边数.
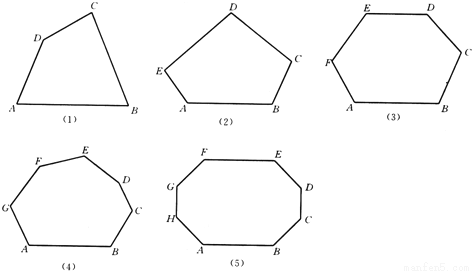
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com