
已知抛物线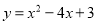 与
与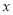 轴相交于点
轴相交于点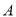 ,
,  (点
(点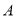 在点
在点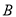 的左侧),顶点为
的左侧),顶点为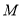 .平移该抛物线,使点
.平移该抛物线,使点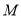 平移后的对应点
平移后的对应点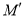 落在
落在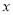 轴上,点
轴上,点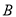 平移后的对应点
平移后的对应点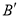 落在
落在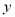 轴上,则平移后的抛物线的解析式为( ).
轴上,则平移后的抛物线的解析式为( ).
A. 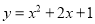 B.
B. 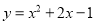 C.
C. 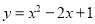 D.
D. 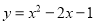
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:初中数学 来源:黄金30题系列 八年级数学 小题好拿分 题型:单选题
若分式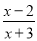 有意义,则
有意义,则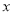 的取值范围是
的取值范围是
A. 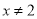 B.
B. 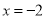 C.
C. 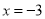 D.
D. 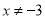
查看答案和解析>>
科目:初中数学 来源:安徽省合肥市2016-17学年度第一学期期末教学质量检测七年级数学试卷 题型:解答题
计算:(?1)2013×| ?3 |?(?2)3+4÷(?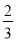 )2
)2
查看答案和解析>>
科目:初中数学 来源:浙江杭州拱墅区文澜中学2018届九年级上学期期中考试数学试卷(含解析) 题型:解答题
如图所示,已知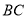 是⊙
是⊙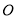 的直径,
的直径, 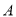 、
、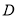 是⊙
是⊙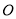 上的两点.
上的两点.

(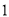 )若
)若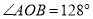 ,求
,求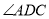 的度数.
的度数.
(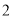 )已知
)已知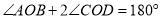 ,连接
,连接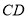 、
、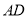 ,其中
,其中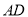 与直径
与直径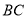 相交于点
相交于点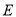 ,求证:
,求证: 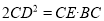 .
.
(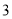 )在(
)在(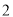 )的条件下,若
)的条件下,若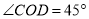 ,求
,求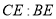 的值.
的值.
查看答案和解析>>
科目:初中数学 来源:浙江杭州拱墅区文澜中学2018届九年级上学期期中考试数学试卷(含解析) 题型:填空题
如图,任两个竖直或水平相邻的点都相距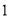 个单位长度.已知线段
个单位长度.已知线段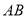 交线段
交线段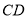 于点
于点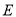 ,则线段
,则线段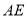 的长是__________.
的长是__________.

查看答案和解析>>
科目:初中数学 来源:浙江杭州拱墅区文澜中学2018届九年级上学期期中考试数学试卷(含解析) 题型:单选题
如图,点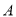 、
、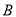 、
、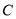 在⊙
在⊙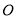 上,
上, 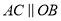 ,
, 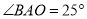 ,则
,则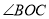 的度数为( ).
的度数为( ).

A. 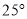 B.
B. 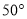 C.
C. 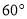 D.
D. 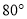
查看答案和解析>>
科目:初中数学 来源:浙江省宁波市2018届九年级上册期末模拟数学试卷 题型:解答题
如图,已知△ABC和△DEC的面积相等,点E在BC边上,DE∥AB交AC于点F,AB=12,EF=9,则DF的长是多少?
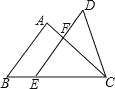
查看答案和解析>>
科目:初中数学 来源:浙江省宁波市2018届九年级上册期末模拟数学试卷 题型:单选题
在一个可以改变体积的密闭容器内装有一定质量的二氧化碳,当改变容器的体积时,气体的密度也会随之改变,密度ρ(单位:kg/m3)是体积V(单位:m3)的反比例函数,它的图象如图所示,当V=10m3时,气体的密度是( )
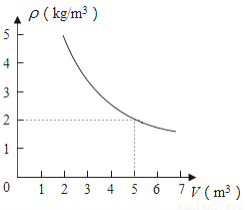
A. 5kg/m3 B. 2kg/m3 C. 100kg/m3 D. 1kg/m3
D 【解析】本题考查的是反比例函数的应用 先根据图象求出反比例函数关系式,即可求得当时,气体的密度。 设反比例函数关系式是, 图象过点(5,2) ,解得, 反比例函数关系式是, 当时,, 故选D。查看答案和解析>>
科目:初中数学 来源:山东省临朐县沂山风景区2017-2018学年八年级上期末模拟数学试卷 题型:单选题
如图,在Rt△ABC中,∠A=90°,∠ABC的平分线BD交AC于点D,AD=3,BC=10,则△BDC的面积是( )
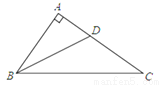
A. 10 B. 15 C. 20 D. 30
B 【解析】【解析】 过D作DE⊥BC于E. ∵∠A=90°,∴DA⊥AB.∵BD平分∠ABC,∴AD=DE=3,∴△BDC的面积是×DE×BC=×10×3=15,故选B.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com