
科目:初中数学 来源:黄金30题系列 八年级数学 小题好拿分 题型:单选题
如图, 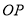 平分
平分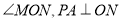 于点
于点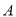 ,点
,点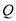 是射线
是射线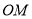 上的一个动点,若
上的一个动点,若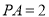 ,则
,则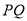 的最小值为( )
的最小值为( )
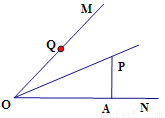
A. 1 B. 2 C. 3 D. 4
B 【解析】试题分析:根据题意点Q是射线OM上的一个动点,要求PQ的最小值,需要找出满足题意的点Q,根据直线外一点与直线上各点连接的所有线段中,垂线段最短,所以我们过点P作PQ垂直OM,此时的PQ最短,然后根据角平分线上的点到角两边的距离相等可得PA=PQ,利用已知的PA的值即可求出PQ的最小值. 【解析】 过点P作PQ⊥OM,垂足为Q,则PQ为最短距离, ∵OP平分∠MON,...查看答案和解析>>
科目:初中数学 来源:安徽省合肥市2016-17学年度第一学期期末教学质量检测七年级数学试卷 题型:单选题
成都市为减少雾霾天气采取了多项措施,如对城区主干道进行绿化.现计划把某一段公路的一侧全部栽上银杏树,要求路的两端各栽一棵,并且每两棵树的间隔相等.如果每隔5米栽1棵,则树苗缺21棵;如果每隔6米栽1棵,则树苗正好用完.设原有树苗x棵,则根据题意列出方程正确的是( )
A. 5(x+21﹣1)=6(x﹣l) B. 5(x+21)=6(x﹣l) C. 5(x+21﹣1)=6x D. 5(x+21)=6x
A 【解析】【解析】 因为设原有树苗x棵,则路的长度为5(x+21﹣1)米,由题意,得 5(x+21﹣1)=6(x﹣1), 故选:A.查看答案和解析>>
科目:初中数学 来源:浙江杭州拱墅区文澜中学2018届九年级上学期期中考试数学试卷(含解析) 题型:填空题
设二次函数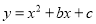 ,当
,当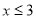 时,总有
时,总有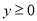 ,当
,当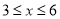 时,总有
时,总有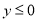 ,则
,则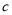 的取值范围是__________.
的取值范围是__________.
查看答案和解析>>
科目:初中数学 来源:浙江杭州拱墅区文澜中学2018届九年级上学期期中考试数学试卷(含解析) 题型:单选题
已知抛物线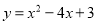 与
与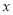 轴相交于点
轴相交于点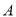 ,
,  (点
(点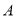 在点
在点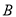 的左侧),顶点为
的左侧),顶点为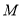 .平移该抛物线,使点
.平移该抛物线,使点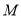 平移后的对应点
平移后的对应点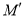 落在
落在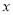 轴上,点
轴上,点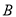 平移后的对应点
平移后的对应点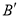 落在
落在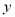 轴上,则平移后的抛物线的解析式为( ).
轴上,则平移后的抛物线的解析式为( ).
A. 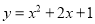 B.
B. 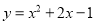 C.
C. 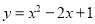 D.
D. 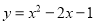
查看答案和解析>>
科目:初中数学 来源:浙江省宁波市2018届九年级上册期末模拟数学试卷 题型:解答题
“蘑菇石”是我国著名的自然保护区梵净山的标志,小明从山脚B点先乘坐缆车到达观景平台DE观景,然后再沿着坡脚为29°的斜坡由E点步行到达“蘑菇石”A点,“蘑菇石”A点到水平面BC的垂直距离为1890m.如图,DE∥BC,BD=1800m,∠DBC=80°,求斜坡AE的长度.(结果精确到0.1m,可参考数据sin29°≈0.4848,sin80°≈0.9848,cos29°≈0.8746,cos80°≈0.1736)
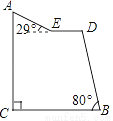
查看答案和解析>>
科目:初中数学 来源:浙江省宁波市2018届九年级上册期末模拟数学试卷 题型:填空题
若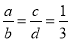 (b+d≠0),则
(b+d≠0),则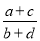 =________
=________
查看答案和解析>>
科目:初中数学 来源:2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷(二) 题型:解答题
问题背景:
如图1:在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°.E,F分别是BC,CD上的点.且∠EAF=60°.探究图中线段BE,EF,FD之间的数量关系.
小王同学探究此问题的方法是,延长FD到点G.使DG=BE.连结AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是 ;
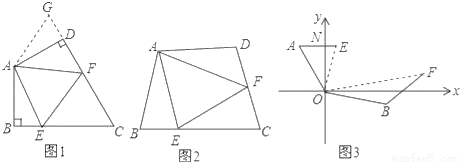
探索延伸:
如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°.E,F分别是BC,CD上的点,且∠EAF=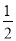 ∠BAD,上述结论是否仍然成立,并说明理由;
∠BAD,上述结论是否仍然成立,并说明理由;
实际应用:
如图3,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西30°的A处,舰艇乙在指挥中心南偏东70°的B处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以60海里/小时的速度前进,舰艇乙沿北偏东50°的方向以80海里/小时的速度前进1.5小时后,指挥中心观测到甲、乙两舰艇分别到达E,F处,且两舰艇之间的夹角为70°,试求此时两舰艇之间的距离.
问题背景:EF=BE+DF; 探索延伸:结论仍然成立,理由见解析; 实际应用:此时两舰艇之间的距离为210海里. 【解析】【解析】 问题背景:EF=BE+DF; 探索延伸:EF=BE+DF仍然成立. 证明如下:如图,延长FD到G,使DG=BE,连接AG, ∵∠B+∠ADC=180°,∠ADC+∠ADG=180°,∴∠B=∠ADG, 在△ABE和△ADG中...查看答案和解析>>
科目:初中数学 来源:山东省临朐县沂山风景区2017-2018学年八年级上期末模拟数学试卷 题型:单选题
直线L是一条河,P,Q是两个村庄.欲在L上的某处修建一个水泵站,向P,Q两地供水,现有如下四种铺设方案,图中实线表示铺设的管道,则所需管道最短的是( ).
A. 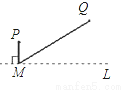 B.
B. 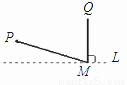
C. 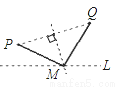 D.
D. 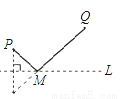
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com