练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    若关于x的方程x2+2（k﹣1）x+k2=0有实数根，则k的取值范围是 ．

    k≤. 【解析】 试题分析：∵关于x的方程x2+2（k﹣1）x+k2=0有实数根， ∴△=[2（k﹣1）]2﹣4k2=﹣8k+4≥0， 解得：k≤．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：湖南省2017-2018学年八年级数学上期末复习检测数学试卷 题型：填空题

    使不等式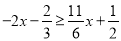成立的最大的整数解是________．

    ﹣1． 【解析】【解析】 去分母，得：﹣12x﹣4≥11x+3，移项、合并，得：﹣23x≥7，系数化为1，得：x≤，∴满足不等式的最大整数解为﹣1，故答案为：﹣1．

    查看答案和解析>>

    科目：初中数学 来源：2017年江苏省苏州市中考数学三模试卷 题型：填空题

    若A（﹣3，y1），B（﹣2，y2），C（1，y3）三点都在y=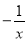的图象上，则yl，y2，y3的大小关系是_____．（用“＜”号填空）

    y3＜y1＜y2 【解析】试题分析：对于反比例函数y=，当k0时，y随着x的增大而增大，x0时y0，x0时y0.

    查看答案和解析>>

    科目：初中数学 来源：福建省建瓯市2018届九年级数学上册期末测试卷 题型：解答题

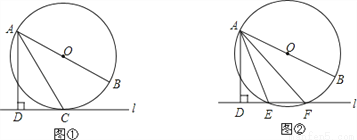
    已知直线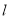与⊙O，AB是⊙O的直径，A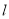D⊥于点D．

    （1）如图①，当直线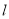与⊙O相切于点C时，若∠DAC=30°，求∠BAC的大小；

    （2）如图②，当直线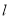与⊙O相交于点E、F时，若∠DAE=18°，求∠BAF的大小．

    （1）30°；（2）18°. 【解析】试题分析：（1）连接OD，易证OC∥AD，所以∠OCA=∠DAC，由因为OA=OC，所以∠OAC=∠OCA； （2）连接BE，AB是⊙O的直径，所以∠AEB=90°，从而可知∠BEF=∠DAE=18°，由圆周角定理可知：∠BAF=∠BEF=18° 试题解析：（1）连接OC、 ∵l是⊙O的切线， ∴OC⊥l， ∵AD⊥l， ...

    查看答案和解析>>

    科目：初中数学 来源：福建省建瓯市2018届九年级数学上册期末测试卷 题型：填空题

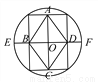
    如图，顺次连接圆内接矩形各边的中点，得到菱形ABCD，若BD＝10，DF＝4，则菱形ABCD的边长为__ __．

    9 【解析】试题分析：如图：连接OG，∵BD=10，DF=4，∴⊙O的半径r=OD+DF=BD+DF=×10+4=9，∴OG=9，在Rt△GOD与Rt△ADO中，OD=OD，AO=GD，∠AOD=∠GDO=90°，∴△AOD≌△GDO，∴OG=AD=9，故答案为：9．

    查看答案和解析>>

    科目：初中数学 来源：福建省建瓯市2018届九年级数学上册期末测试卷 题型：单选题

    如图，在4×4的正方形网格中，每个小正方形的边长为1，若将△AOC绕点O顺时针旋转90°得到△BOD，则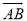的长为（ ）

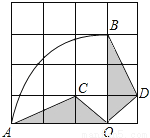
    A. π B. 6π C. 3π D. 1．5π

    D 【解析】试题分析： 的长==1.5π． 故选D．

    查看答案和解析>>

    科目：初中数学 来源：2017年吉林省长春市中考数学模拟试卷 题型：解答题

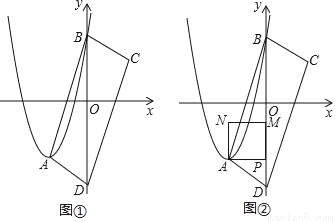
    如图①，在平面直角坐标系中，抛物线y=x2﹣2mx+m2+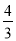m的顶点为A，与y轴交于点B．当抛物线不经过坐标原点时，分别作点A、B关于原点的对称点C、D，连结AB、BC、CD、DA．

    （1）分别用含有m的代数式表示点A、B的坐标．

    （2）判断点B能否落在y轴负半轴上，并说明理由．

    （3）连结AC，设l=AC+BD，求l与m之间的函数关系式．

    （4）过点A作y轴的垂线，交y轴于点P，以AP为边作正方形APMN，MN在AP上方，如图②，当正方形APMN与四边形ABCD重叠部分图形为四边形时，直接写出m的取值范围．

    （1）A（m， m），（0，m2+m）；（2）点B能落在y轴负半轴上；（3）l=2m2﹣m；（4）m＜﹣1． 【解析】试题分析： （1）①把配方化为顶点式，可得顶点A的坐标；②在中，由可得，由此可得点B的坐标； （2）由顶点A的位置可得“”；由点B的坐标为可知，若点B在轴负半轴，则有，两者结合可解得： 时，点B就在轴负半轴； （3）由题意可知： =AC+BD=2OA+OB，...

    查看答案和解析>>

    科目：初中数学 来源：2017年吉林省长春市中考数学模拟试卷 题型：单选题

    如图，A、B、C、D是⊙O上的四点，BD为⊙O的直径，若四边形ABCO是平行四边形，则∠ADB的大小为（　　）

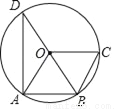
    A. 30° B. 45° C. 60° D. 75°

    A 【解析】∵四边形ABCO是平行四边形，且OA=OC， ∴四边形ABCO是菱形， ∴AB=OA=OB， ∴△OAB是等边三角形， ∴∠AOB=60°， ∵BD是⊙O的直径， ∴点B、D、O在同一直线上， ∴∠ADB=∠AOB=30°. 故选A.

    查看答案和解析>>

    科目：初中数学 来源：江苏省苏州市2017年中考数学二模试卷 题型：填空题

    如图．在等边△ABC中，AC=8，点D，E，F分别在三边AB，BC，AC上，且AF=2，FD⊥DE，∠DFE=60°，则AD的长为________．

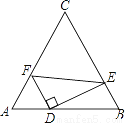
    3 【解析】 ∵∠DFE=60°， ∴∠1+∠2+60°=180°， ∴∠2=120°?∠1， 在等边△ABC中,∠A=∠C=60°， ∴∠A+∠1+∠3=180°， ∴∠3=180°?∠A?∠1=120°?∠1， ∴∠2=∠3， 又∵∠A=∠C， ∴△ADF∽△CFE， ∴ADCF=DFEF， ∵FD⊥DE,∠DFE=60°...

    查看答案和解析>>

    同步练习册答案