练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    抛物线y=x2﹣2的顶点坐标是（ ）

    A. （0，2） B. （0，﹣2） C. （﹣2，0） D. （2，0）

    B 【解析】试题分析：对于二次函数的顶点坐标为(m，k)，则本题中函数的顶点坐标为(0，-2)，故选B．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：山东省2017-2018学年八年级上期末模拟数学试卷 题型：解答题

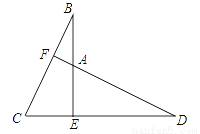
    已知：如图，BE⊥CD，BE=DE，BC=DA．

    求证：（1）△BEC≌△DAE；

    （2）DF⊥BC．

    （1）证明见解析；（2）证明见解析． 【解析】试题分析：此题主要考查学生对全等三角形的判定及性质的理解及运用．全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具．在判定三角形全等时，关键是选择恰当的判定条件． （1）根据已知利用HL即可判定△BEC≌△DEA； （2）根据第（1）问的结论，利用全等三角形的对应角相等可得到∠B=∠D，从而不难求得DF⊥BC． 试...

    查看答案和解析>>

    科目：初中数学 来源：吉林省长春汽车经济技术开发区2017-2018学年八年级上学期期末教学质量跟踪测试数学试卷 题型：单选题

    如图是一个三级台阶，它的每一级的长、宽、高分别为20dm、3dm、2dm.A和B是这个台阶上两个相对的端点，点A处有一只蚂蚁，想到点B处去吃可口的食物，则蚂蚁沿着台阶面爬行到点B的最短路程为（ ）

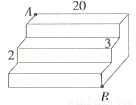
    A. 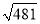dm B. 20dm C. 25dm D. 35dm

    C 【解析】试题解析：三级台阶平面展开图为长方形，长为20dm，宽为（2+3）×3dm， 则蚂蚁沿台阶面爬行到B点最短路程是此长方形的对角线长． 设蚂蚁沿台阶面爬行到B点最短路程为xdm， 由勾股定理得：x2=202+[（2+3）×3]2=252， 解得：x=25（dm）． 故选C．

    查看答案和解析>>

    科目：初中数学 来源：安徽省2018届九年级上学期第二次月考数学试卷 题型：填空题

    已知二次函数y=ax2+bx+c（a≠0），其中a，b，c满足a+b+c=0和9a﹣3b+c=0，则该二次函数图象的对称轴是直线 ．

    x=﹣1． 【解析】 试题分析：解方程求出a，b的值，再根据对称轴公式即可求出该二次函数图象的对称轴． 【解析】 方程9a﹣3b+c=0减去方程a+b+c=0， 可得8a﹣4b=0， 根据对称轴公式整理得：对称轴为x==﹣1． 故该二次函数图象的对称轴是直线x=﹣1．

    查看答案和解析>>

    科目：初中数学 来源：安徽省2018届九年级上学期第二次月考数学试卷 题型：单选题

    如图，若∠1=∠2=∠3，则图中的相似三角形有（ ）

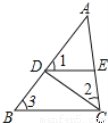
    A. 1对 B. 2对 C. 3对 D. 4对

    D 【解析】试题分析：根据已知及相似三角形的判定定理，找出题中存在的相似三角形即可． 【解析】 ∵∠1=∠2，∠C=∠C ∴△ACE∽△ECD ∵∠2=∠3 ∴DE∥AB ∴△BCA∽△ECD ∵△ACE∽△ECD，△BCA∽△ECD ∴△ACE∽△BCA ∵DE∥AB ∴∠AED=∠BAE ∵∠1=∠3 ∴△AED∽△BA...

    查看答案和解析>>

    科目：初中数学 来源：2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷 题型：解答题

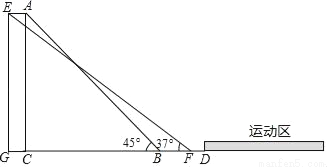
    某学校为增加体育馆观众坐席数量，决定对体育馆进行施工改造．如图，为体育馆改造的截面示意图．已知原座位区最高点A到地面的铅直高度AC长度为15米，原坡面AB的倾斜角∠ABC为45°，原坡脚B与场馆中央的运动区边界的安全距离BD为5米．如果按照施工方提供的设计方案施工，新座位区最高点E到地面的铅直高度EG长度保持15米不变，使A、E两点间距离为2米，使改造后坡面EF的倾斜角∠EFG为37°．若学校要求新坡脚F需与场馆中央的运动区边界的安全距离FD至少保持2.5米（即FD≥2.5），请问施工方提供的设计方案是否满足安全要求呢？请说明理由．（参考数据：sin37°≈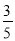，tan37°≈）

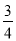    施工方提供的设计方案不满足安全要求． 【解析】试题分析： 在Rt△ABC中，由∠ACB=90°，AC=15m，∠ABC=45°可求得BC=15m；在Rt△EGD中，由∠EGD=90°，EG=15m，∠EFG=37°，可解得GF=20m；通过已知条件可证得四边形EACG是矩形，从而可得GC=AE=2m；这样可解得：DF=GC+BC+BD-GF=2+15+5-20=2<2.5，由此可知：“...

    查看答案和解析>>

    科目：初中数学 来源：2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷 题型：填空题

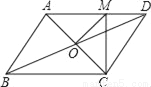
    如图，□ABCD的周长为16cm，AC、BD交于点O，且AD＞CD，过O作OM⊥AC，交AD于点M，则△CDM的周长为_____cm．

    8 【解析】∵四边形ABCD是平行四边形， ∴OA=OC， ∵OM⊥AC， ∴AM=CM， ∴△CDM的周长为：CD+DM+CM=CD+DM+AM=CD+AD， ∵□ABCD的周长为16cm， ∴CD+AD=8cm， ∴△CDM的周长为8cm． 故答案为：8．

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年江苏省苏州市初三上期中试卷数学试卷 题型：解答题

    已知抛物线．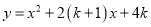

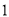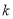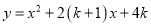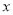    （）求证：不论取何值，抛物线与轴有交点．

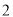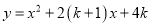    （）若抛物线与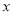轴有两个交点，且这两个交点分别在直线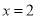的两侧，求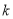的取值范围．

    （1）证明见解析；（2）． 【解析】试题分析：（1）证明△≥0即可得结论；（2）根据题意可知当x=2时，y小于0，把x=2代入解析式，列出不等式，解不等式即可. 试题解析： （） ． ∴不论取何值，抛物线与轴均有交点． （）根据题意可知当x=2时，y＜0， ∴4+4（k+1）+4k＜0，， 所以．

    查看答案和解析>>

    科目：初中数学 来源：2017年内蒙古乌兰察布市中考数学一模试卷 题型：单选题

    如图，在正方形ABCD中，对角线AC，BD交于点O，折叠正方形ABCD，使AB边落在AC上，点B落在点H处，折痕AE分别交BC于点E，交BO于点F，连结FH，则下列结论（1）AD=DF；（2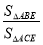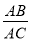）=；（3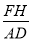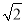）=﹣1；（4）四边形BEHF为菱形．正确的有几个（　　）

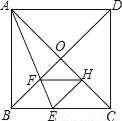
    A. 1个 B. 2个 C. 3个 D. 4个

    D 【解析】试题解析：(1)∵在正方形纸片ABCD中，折叠正方形纸片ABCD，使AB落在AC上，点B恰好与AC上的点H重合， ∴AD=DF， 故(1)正确； (2)∵在正方形纸片ABCD中，折叠正方形纸片ABCD，使AB落在AC上，点B恰好与AC上的点H重合， ∴△ABE≌△AEH， ∴BE=EH， 故(2)正确； (3)∵在正方形纸片ABCD中，折...

    查看答案和解析>>

    同步练习册答案