练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    下列说法正确的有(   )

    　 ①不相交的两条直线是平行线；②在同一平面内，两条直线的位置关系有两种；

    　 ③若线段AB与CD没有交点，则AB∥CD；④若a∥b，b∥c，则a与c不相交．

    A. 1个 B. 2个 C. 3个 D. 4个

    B 【解析】①错，在同一平面内时①才成立；②正确；③错，两线段平行是指它们所在直线没交点；④正确．故选B．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：北师大版数学七年级下册第一章整式乘法1.7整式的除法课时练习 题型：单选题

    （4x2y4+4x2z ） ÷（2x）2等于（ ）

    A. 4y4+z B. －y4+z C. y4+x2z D. y4+z

    D 【解析】（4x2y4+4x2z ） ÷（2x）2=（4x2y4+4x2z ） ÷4x2=4x2y4÷4x2+4x2z ÷4x2= y4+x2z， 故选：D.

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级下册 2.2 探索直线平行的条件（1） 同步练习 题型：解答题

    如图所示，直线AB，CD被直线EF所截，如果∠1＝70°，∠2＝110°，试说明：AB//CD.

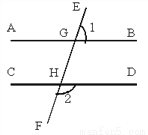
    证明见解析. 【解析】试题分析：由邻补角定义得出∠BGF＝110°，再由同位角相等，两直线平行，即可证得AB∥CD. 试题解析：∵∠1＝70°， ∴∠BGF＝180°－∠1=180°－70°=110°， ∴∠2＝110°， ∴∠2＝∠BGF， ∴AB∥CD（同位角相等，两直线平行）

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下册 第二章 相交线与平行线 2.2 探索直线平行的条件 同位角及平行公理 同步课堂练习题 题型：解答题

    如图，三角形ABC中，已知∠C=45°，∠ADB=90°，DE为∠ADB的平分线，DE与CA平行吗？说明你的理由．

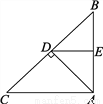
    证明见解析 【解析】分析：由DE为∠ADB的平分线，得∠BDE=∠ADB=45°，则∠BDE=∠C=45°，根据同位角相等判定两直线平行，可得DE∥CA. 本题解析： 【解析】 DE∥CA，因为∠ADB=90°，DE平分∠ADB，所以∠BDE=∠ADB=45°，又因为∠C=45°，所以∠BDE=∠C，所以DE∥CA.

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下册 第二章 相交线与平行线 2.2 探索直线平行的条件 同位角及平行公理 同步课堂练习题 题型：填空题

    如图，具有∠1与____这样位置关系的角称为同位角，图中的同位角还有∠3与____，∠5与____，∠7与____.

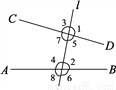
    ∠2 ∠4 ∠6 ∠8 【解析】根据同位角的判定：如图，具有∠1与∠2这样位置关系的角称为同位角， 图中的同位角还有∠3与∠4，∠5与∠6，∠7与∠8 故答案为： ∠2 , ∠4 , ∠6 ,∠8 .

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下册 第二章 相交线与平行线 2.2 探索直线平行的条件 同位角及平行公理 同步课堂练习题 题型：单选题

    如图，直线AB、CD被直线EF所截，则∠AMN的同位角是( )

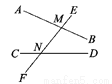
    A. ∠CNM B. ∠CNF C. ∠DNF D. ∠DNM

    B 【解析】∵直线AB、CD被直线EF所截， ∴只有∠AMN与∠CNF在截线EF的同侧，且在AB和CD的同旁， 即∠CNF是∠AMN的同位角。 故选B.

    查看答案和解析>>

    科目：初中数学 来源：人教版2017-2018学年九年级下册数学全册综合测试卷 题型：填空题

    如果函数y=kxk﹣2是反比例函数，那么k=________ ，此函数的解析式是________ ．

    1； y= 【解析】试题分析：根据反比例函数的定义列出方程求解，再根据它的性质决定解的取舍． 【解析】 根据题意，k﹣2=﹣1，解得k=1，且k≠0， ∴函数的解析式为：y=． 故答案为：1，y=．

    查看答案和解析>>

    科目：初中数学 来源：人教版2017-2018学年九年级下册数学全册综合测试卷 题型：单选题

    下列说法正确的是（　　）

    A. 求sin30°的按键顺序是 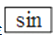、30、=

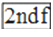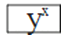    B. 求23的按键顺序 、2、 、3、=

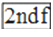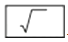    C. 求的按键顺序是、 、8、=

    D. 已知sinA=0.5018，用计算器求锐角A的大小，按键顺序是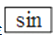、、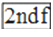0.5018、=

    A 【解析】求sin30°的按键顺序是、30、=，A正确； 求23的按键顺序2、、3、=，B错误； 求的按键顺序是、8、=，C错误； 已知sinA=0.5018,用计算器求锐角A的大小,按键顺序是先按shift键、0.5018、=，D错误， 故选：A.

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年九年级数学北师大版上册 全册综合测试卷1 题型：单选题

    如图，在△ABC中，DE∥BC，AD=6，DB=3，AE=4，则EC的长为（　　）

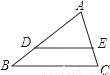
    A. 1 B. 2 C. 3 D. 4

    B 【解析】试题分析：根据平行线分线段成比例可得，代入计算可得： ，即可解EC=2， 故选：B．

    查看答案和解析>>

    同步练习册答案