
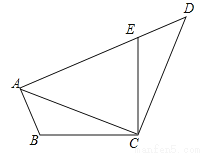
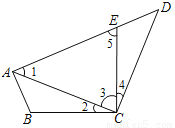
如图,已知在四边形ABCD中,点E在AD上,∠BCE=∠ACD=90°,∠BAC=∠D,BC=CE.
(1)求证:AC=CD;
(2)若AC=AE,求∠DEC的度数.
【答案】(1)证明见解析;(2)112.5°.
【解析】试题分析: 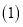 根据同角的余角相等可得到
根据同角的余角相等可得到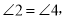 结合条件
结合条件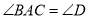 ,再加上
,再加上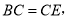 可证得结论;
可证得结论;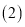 根据
根据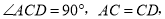 得到
得到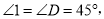 根据等腰三角形的性质得到
根据等腰三角形的性质得到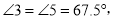 由平角的定义得到
由平角的定义得到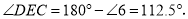
试题解析:  证明:
证明:
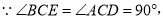
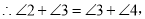
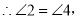
在△ABC和△DEC中,  ,
,
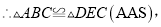
(2)∵∠ACD=90°,AC=CD,
∴∠1=∠D=45°,
∵AE=AC,
∴∠3=∠5=67.5°,
∴∠DEC=180°-∠5=112.5°.
【题型】解答题
【结束】
21
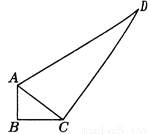
一个零件的形状如图所示,工人师傅按规定做得∠B=90°,
AB=3,BC=4,CD=12,AD=13,假如这是一块钢板,你能帮工人师傅计算一下这块钢板的面积吗?
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2017年广西防城港市中考数学模拟试卷 题型:填空题
某校决定从三名男生和两名女生中选出两名同学担任校艺术节文艺演出专场的主持人,则选出的恰为一男一女的概率是 .
【解析】 试题分析:某校决定从三名男生和两名女生中选出两名同学担任校艺术节文艺演出专场的主持人,假如所选同学全是男生有3种情况,全是女生有1种,一男一女有=6种情况;则选出的恰为一男一女的概率=查看答案和解析>>
科目:初中数学 来源:山东省诸城市2017-2018学年七年级上学期第二次月考数学试卷 题型:解答题
某商场将M品牌服装每套按进价的2倍进行销售,恰逢“春节”来临,为了促销,他将售价提高了50元再标价,打出了“大酬宾,八折优惠”的牌子,结果每套服装的利润是进价的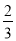 ,该老板到底给顾客优惠了吗?说出你的理由.
,该老板到底给顾客优惠了吗?说出你的理由.
查看答案和解析>>
科目:初中数学 来源:山东省诸城市2017-2018学年七年级上学期第二次月考数学试卷 题型:单选题
下列曲线中不能表示y是x的函数的是( )
A. 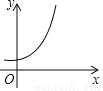 B.
B. 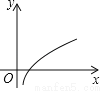 C.
C. 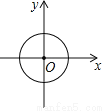 D.
D. 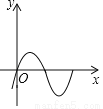
查看答案和解析>>
科目:初中数学 来源:江苏省盐城市2017-2018学年八年级12月联合质量调研数学试卷 题型:解答题
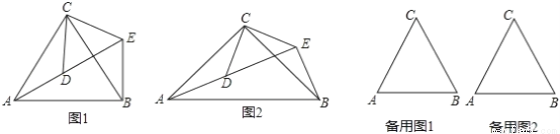
(1)问题发现:如图1,△ACB和△DCE均为等边三角形,当△DCE旋转至点A,D,E在同一直线上,连接BE.
填空:① ∠AEB的度数为_______;②线段AD、BE之间的数量关系是______.
(2)拓展研究:
如图2,△ACB和△DCE均为等腰三角形,且∠ACB=∠DCE=90°,点A、D、E在同一直线上,若AE=15,DE=7,求AB的长度.
(3)探究发现:
图1中的△ACB和△DCE,在△DCE旋转过程中当点A,D,E不在同一直线上时,设直线AD与BE相交于点O,试在备用图中探索∠AOE的度数,直接写出结果,不必说明理由.
【答案】(1)60°.AD=BE;(2)AB=17;(3)∠AOE的度数是60°或120°.
【解析】试题分析:(1)由条件易证△ACD≌△BCE,从而得到:AD=BE,∠ADC=∠BEC.由点A,D,E在同一直线上可求出∠ADC,从而可以求出∠AEB的度数.
(2)仿照(1)中的解法可求出∠AEB的度数,证出AD=BE;由△DCE为等腰直角三角形及CM为△DCE中DE边上的高可得CM=DM=ME,从而证到AE=2CH+BE.
(3)由(1)知△ACD≌△BCE,得∠CAD=∠CBE,由∠CAB=∠ABC=60°,可知∠EAB+∠ABE=120°,根据三角形的内角和定理可知∠AOE=60°.
试题解析:(1)①∵△ACB和△DCE均为等边三角形,
∴CA=CB,CD=CE,∠ACB=∠DCE=60°.
∴∠ACD=∠BCE.
在△ACD和△BCE中,
 ,
,
∴△ACD≌△BCE(SAS).
∴∠ADC=∠BEC.
∵△DCE为等边三角形,
∴∠CDE=∠CED=60°.
∵点A,D,E在同一直线上,
∴∠ADC=120°.
∴∠BEC=120°.
∴∠AEB=∠BEC?∠CED=60°.
故答案为:60°.
②∵△ACD≌△BCE,
∴AD=BE.
故答案为:AD=BE.
(2)∵△ACB和△DCE均为等腰直角三角形,
∴CA=CB,CD=CE,∠ACB=∠DCE=90°.
∴∠ACD=∠BCE.
在△ACD和△BCE中,
 ,
,
∴△ACD≌△BCE(SAS).
∴AD=BE=AE-DE=8,∠ADC=∠BEC,
∵△DCE为等腰直角三角形,
∴∠CDE=∠CED=45°.
∵点A,D,E在同一直线上,
∴∠ADC=135°.
∴∠BEC=135°.
∴∠AEB=∠BEC?∠CED=90°.
∴AB=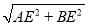 =17;
=17;
(3)由(1)知△ACD≌△BCE,
∴∠CAD=∠CBE,
∵∠CAB=∠CBA=60°,
∴∠OAB+∠OBA=120°
∴∠AOE=180°?120°=60°,
同理求得∠AOB=60°,
∴∠AOE=120°,
∴∠AOE的度数是60°或120°.
点睛:本题考查了等边三角形的性质、等腰三角形的性质、直角三角形斜边上的中线等于斜边的一半、三角形全等的判定与性质等知识,考查了运用已有的知识和经验解决问题的能力.
【题型】解答题
【结束】
26
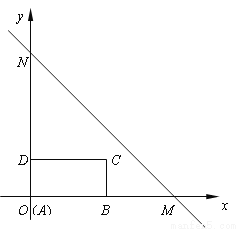
如图,直线MN:y=-x+b与x轴交于点M(4,0),与y轴交于点N,长方形ABCD的边AB在x轴上,AB=2,AD=1.长方形ABCD由点A与点O重合的位置开始,以每秒1个单位长度的速度沿x轴正方向作匀速直线运动,当点A与点M重合时停止运动.设长方形运动的时间为t秒,长方形ABCD与△OMN重合部分的面积为S.
(1)求直线MN的解析式;
(2)当t=1时,请判断点C是否在直线MN上,并说明理由;
(3)请求出当t为何值时,点D在直线MN上;
(4)直接写出在整个运动过程中S与t的函数关系式
查看答案和解析>>
科目:初中数学 来源:江苏省盐城市2017-2018学年八年级12月联合质量调研数学试卷 题型:填空题
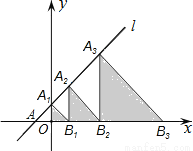
如图,在平面直角坐标系中,直线l:y=x+2交x轴于点A,交y轴于点A1,点A2,A3,…在直线l上,点B1,B2,B3,…在x轴的正半轴上,若△A1OB1,△A2B1B2,△A3B2B3,…,依次均为等腰直角三角形,直角顶点都在x轴上,则第n个等腰直角三角形AnBn﹣1Bn顶点Bn的横坐标为________________.
查看答案和解析>>
科目:初中数学 来源:江苏省盐城市2017-2018学年八年级12月联合质量调研数学试卷 题型:填空题
点P(1,-2)关于x轴对称的点的坐标是_____.
(1,2) 【解析】点P(1,-2)关于x轴对称的点的坐标是(1,2). 故答案为(1,2).查看答案和解析>>
科目:初中数学 来源:2016-2017学年陕西师大附中七年级(下)第一次月考数学试卷 题型:填空题
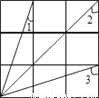
如图所示的方格中,∠1+∠2+∠3=_____度.
查看答案和解析>>
科目:初中数学 来源:四川省遂宁市黄泥学校2016-2017学年上期八年级期中测评数学试卷 题型:单选题
下列从左边到右边的变形,属于因式分解的是( )
A. 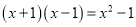 B.
B. 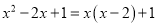
C. 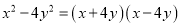 D.
D. 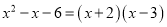
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com