练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，过点A（2，0）的两条直线l1，l2分别交y轴于点B，C，其中点B在原点上方，点C在原点下方，已知AB= ．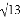

    （1）求点B的坐标；

    （2）若△ABC的面积为4，求直线l2的解析式．

    （1）点B的坐标为（0，3）；（2）l2的解析式为y=x-1. 【解析】（1）先根据勾股定理求得BO的长，再写出点B的坐标；（2）先根据△ABC的面积4，求得CO的长，再根据点A、C的坐标运用待定系数法求得直线l2的解析式. 【解析】 （1）∵点A（2，0），AB= ∴BO==3 ∴点B的坐标为（0，3）； （2）∵△ABC的面积为4 ∴×BC×AO=4 ∴×BC×...
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：广东省广州市天河区2017-2018学年七年级上学期期末考试数学试卷 题型：填空题

    某地1月份的平均气温是零下5℃，用负数表示这个温度是________．

    －5℃ 【解析】某地1月份的平均气温是零下5℃，用负数表示这个温度是－5℃， 故答案为：－5℃.

    查看答案和解析>>

    科目：初中数学 来源：四川省遂宁市蓬溪县2018届九年级上学期期末考试数学试卷 题型：解答题

    学习了“锐角三角函数”后，刘老师在“五环四互”的“检测互评”环节出了如下题目，请解答：如图，已知：△ABC中，BD、CE是高.

    （1）求证：AE·AB=AD·AC；

    （2）若AD、AB的长是一元二次方程x2－8x＋15=0的根，求sin∠ACE的值.

    （1）证明见解析；（2）sin∠ACE= 【解析】试题分析：（1）证明△ABD∽△ACE是解决AD•AC=AE•AB的途径； （2）解方程x2－8x＋15=0得AD=3,AB=5,进而求得sin∠ABD=，由（1）知∠ACE= ∠ABD，故可得结论. 试题解析：（1）证明：BD⊥AC，CE⊥AB⇒∠ADB=∠AEC=90°和∠A=∠A⇒△ABD∽△ACE⇒AD：AE=AB：AC⇒...

    查看答案和解析>>

    科目：初中数学 来源：四川省遂宁市蓬溪县2018届九年级上学期期末考试数学试卷 题型：单选题

    等腰梯形的腰长是5cm，中位线的长是4cm，这个等腰梯形的周长是（ ）

    A. 9cm B. 13cm C. 18cm D. 20cm

    C 【解析】试题解析：∵等腰梯形ABCD的中位线EF的长为4， ∴AB+CD=2×4=8． 又∵腰AD的长为5， ∴这个等腰梯形的周长为AB+CD+AD+BC=8+5+5=18． 故选C.

    查看答案和解析>>

    科目：初中数学 来源：江苏省盐城市2016-2017学年八年级上学期期末考试数学试卷 题型：解答题

    一张矩形纸片，剪下一个正方形，剩下一个矩形，称为第一次操作；在剩下的矩形纸片中再剪下一个正方形，剩下一个矩形，称为第二次操作；…；若在第n次操作后，剩下的矩形为正方形，则称原矩形为n阶奇异矩形．

    （1）如图1，矩形ABCD中，若AB=3，BC=9，则称矩形ABCD为　　阶奇异矩形．

    （2）如图2，矩形ABCD长为7，宽为3，它是奇异矩形吗？如果是，请写出它是几阶奇异矩形，并在图中画出裁剪线；如果不是，请说明理由．

    （3）已知矩形ABCD的一边长为20，另一边长为a（a＜20），且它是3阶奇异矩形，请画出矩形ABCD及裁剪线的示意图，并在图的下方直接写出a的值．

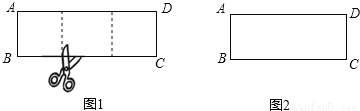
    （1）2 （2）矩形ABCD是4阶奇异矩形 （3）图形见解析 【解析】试题分析：（1）已知经过2次操作后剩下的矩形为正方形， 所以矩形ABCD为2阶奇异矩形. （1）根据已知操作步骤画出即可；（2）根据已知得出符合条件的有4种情况，画出图形即可． 【解析】 （1）∵第2次操作后，剩下的矩形为正方形， ∴ 矩形ABCD为2阶奇异矩形 （2）矩形ABCD是4阶奇异矩形，裁剪线...

    查看答案和解析>>

    科目：初中数学 来源：江苏省盐城市2016-2017学年八年级上学期期末考试数学试卷 题型：填空题

    如图，在?ABCD中，E为边CD上一点，将△ADE沿AE折叠至△AD′E处，AD′与CE交于点F．若∠B=52°，∠DAE=20°，则∠FED′的大小为________．

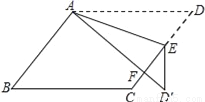
    36° 【解析】试题分析：∵四边形ABCD是平行四边形， ∴∠D＝∠B＝52°， 由折叠的性质得：∠D′＝∠D＝52°，∠EAD′＝∠DAE＝20°， ∴∠AEF＝∠D＋∠DAE＝52°＋20°＝72°，∠AED′＝180°－∠EAD′－∠D′＝108°， ∴∠FED′＝108°－72°＝36°； 故答案为：36°．

    查看答案和解析>>

    科目：初中数学 来源：江苏省盐城市2016-2017学年八年级上学期期末考试数学试卷 题型：填空题

    在一组数据中，随机抽取50个作为样本进行统计，在频数分布表中，54.5～57.5这一组的频率是0.12，那么这个样本中的数据落在54.5～57.5之间的有__个．

    6 【解析】50×0.12=6（个）.

    查看答案和解析>>

    科目：初中数学 来源：河南省2017-2018学年七年级上学期期末考试数学试卷 题型：填空题

    已知点O在直线AB上，且线段AB=4cm，线段OB=6cm，E,F分别是OA，OB的中点，则线段EF=_____cm.

    2 【解析】因为点O在直线AB上,且线段AB=4cm,线段OB=6cm,所以点O在线段AB延长线上或在线段BA延长线上,当点O在线段AB延长线上,根据中点的性质AO=4+6=10cm,因为点E是OA的中点,所以OE=5cm,点F是OB的中点,OF=3cm,所以EF=5-3=2cm,当点O在线段BA延长线上时,AO=2cm,OB=6cm,因为点E是OA的中点,所以OE=1cm,点F是OB的中点...

    查看答案和解析>>

    科目：初中数学 来源：安徽省2017-2018学年九年级上学期期末试卷数学 题型：解答题

    某宾馆有50个房间供游客居住，当每个房间定价120元时，房间会全部住满，当每个房间每天的定价每增加10元时，就会有一个房间空闲，如果游客居住房间，宾馆需对每个房间每天支出20元的各种费用，设每个房间定价增加10x元(x为整数)．

    (1)直接写出每天游客居住的房间数量y与x的函数关系式；

    (2)设宾馆每天的利润为W元，当每个房间定价为多少元时，宾馆每天所获利润最大，最大利润是多少？

    (3)某日，宾馆了解当天的住宿情况，得到以下信息：

    ①当日所获利润不低于5000元，

    ②宾馆为游客居住的房间共支出费用没有超过600元，

    ③每个房间刚好住满2人．

    问：这天宾馆入住的游客人数最少有多少人？

    （1）y=50-x，（0≤x≤50，且x为整数）；（2）每间房价定价为320元时，宾馆每天所获利润最大，最大利润是9000元；（3）20人 【解析】试题分析：（1）根据每天游客居住的房间数量等于50﹣减少的房间数即可解决问题． （2）构建二次函数，利用二次函数的性质解决问题． （3）根据条件列出不等式组即可解决问题． 试题解析：（1）根据题意，得：y=50﹣x，（0≤x≤5...

    查看答案和解析>>

    同步练习册答案