
解分式方程:
(1)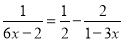
(2)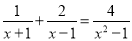 .
.
科目:初中数学 来源:浙江省杭州市余杭区英特外国语学校2017-2018学年八年级上学期期中考试数学试卷 题型:解答题
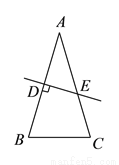
如图所示,等腰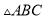 的周长为
的周长为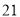 ,底边为
,底边为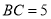 ,
, 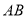 的垂直平分线
的垂直平分线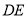 交
交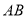 于点
于点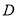 ,交
,交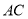 于点
于点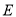 .
.
(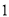 )求
)求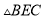 的周长;
的周长;
(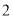 )若
)若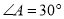 ,
, 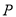 为
为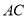 上一点,连结
上一点,连结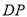 ,
, 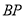 ,求
,求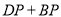 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源:河南省邓州市2018届九年级上学期期中质量评估---数学试卷word版 题型:单选题
一元二次方程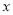 (
(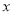 -3)=3-
-3)=3- 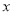 的根是 ( )
的根是 ( )
A. -3 B. 0 C. 1和3 D. 3和-1
D 【解析】【解析】 x(x-3)+(x-3)=0,(x+1)(x-3) =0,∴x=-1或3.故选D.查看答案和解析>>
科目:初中数学 来源:山东省日照市莒县2017-2018学年七年级(上)期中数学试卷 题型:单选题
一台电视机成本价为a元,销售价比成本价增加25%,因库存积压,所以就按销售价的70%出售.那么每台实际售价为( )
A. (1+25%)(1+70%)a元 B. 70%(1+25%)a元
C. (1+25%)(1﹣70%)a元 D. (1+25%+70%)a元
B 【解析】试题解析:可先求销售价(1+25%)a元,再求实际售价70%(1+25%)a元.故选B.查看答案和解析>>
科目:初中数学 来源:2017年山东省枣庄市中考数学模拟试卷(一) 题型:解答题
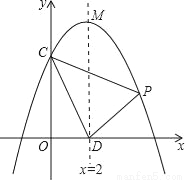
如图:抛物线y=ax2+bx+c交y轴于点C(0,4),对称轴x=2与x轴交于点D,顶点为M,且DM=OC+OD,
(1)求抛物线的解析式;
(2)设点P(x,y)是第一象限内该抛物线上的一个动点,△PCD的面积为S,求S关于x的函数关系式,写出自变量x的取值范围,并求当x取多少时,S的值最大,最大是多少?
查看答案和解析>>
科目:初中数学 来源:北京市延庆县第一学区2017-2018学年八年级(上)期中数学试卷 题型:填空题
若关于x的方程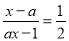 的解是x=2,则a=_____.
的解是x=2,则a=_____.
查看答案和解析>>
科目:初中数学 来源:北京市延庆县第一学区2017-2018学年八年级(上)期中数学试卷 题型:填空题
2的平方根是_____, 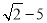 的绝对值是_____.
的绝对值是_____.
查看答案和解析>>
科目:初中数学 来源:吉林省长春市五校2018届九年级(上)期中数学试卷 题型:解答题
(6分)如图,学校课外生物小组的试验园地是长40 m、宽20m的矩形,为便于管理,现要在中间开辟一横两纵三条等宽的小道,要使种植面积为648m2,求小道的宽.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期苏州市八年级数学期末复习综合检测卷 题型:单选题
在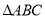 和
和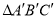 中,
中, 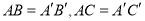 ,高
,高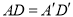 ,则
,则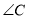 和
和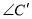 的关系是( )
的关系是( )
A. 相等 B. 互补
C. 相等或互补 D. 以上都不对
C 【解析】试题解析:当∠C′为锐角时,如图1所示, ∵AC=A′C′,AD=A′D′,AD⊥BC,A′D′⊥B′C′, ∴Rt△ADC≌Rt△A′D′C′, ∴∠C=∠C′; 当∠C为钝角时,如图3所示, ∵AC=A′C′,AD=A′D′,AD⊥BC,A′D′⊥B′C′, ∴Rt△ACD≌Rt△A′C′D′, ∴∠C=∠A′C′D′, ∴∠C+∠A′C′B′=180...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com