
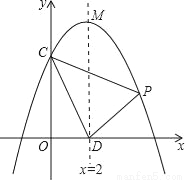
��ͼ��������y=ax2+bx+c��y���ڵ�C��0��4�����Գ���x=2��x�ύ�ڵ�D������ΪM����DM=OC+OD��
��1���������ߵĽ���ʽ��
��2�����P��x��y���ǵ�һ�����ڸ��������ϵ�һ�����㣬��PCD�����ΪS����S����x�ĺ�����ϵʽ��д���Ա���x��ȡֵ��Χ������xȡ����ʱ��S��ֵ�������Ƕ��٣�

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ���㽭ʡ�������������̳�����2017-2018ѧ����꼶��ѧ�����п�����ѧ�Ծ� ���ͣ���ѡ��
��Ӧ���⡰��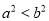 ����
����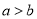 ������������
������������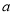 ��
�� 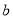 ��ֵ�У���˵����������Ǽ�������ǣ� ����
��ֵ�У���˵����������Ǽ�������ǣ� ����
A. 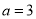 ��
�� 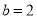 B.
B. 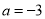 ��
�� 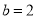 C.
C. 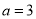 ��
�� 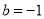 D.
D. 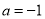 ��
�� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������2018����꼶��ѧ��������������---��ѧ�Ծ�word�� ���ͣ���ѡ��
�������x��һԪ���η�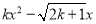 +1=0����������ȵ�ʵ��������ôk��ȡֵ��Χ�ǣ�������
+1=0����������ȵ�ʵ��������ôk��ȡֵ��Χ�ǣ�������
A. -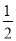 ��k��
��k��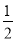 ��k��0 B. k��
��k��0 B. k��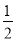 ��k��0
��k��0
C. -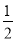 ��k��
��k��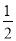 D. k��
D. k��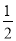
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡ����������2017-2018ѧ�����꼶���ϣ�������ѧ�Ծ� ���ͣ���ѡ��
����˵��������aΪ����������a��ʾ������������a2=����a��2������|a|��b����a2��b2������a+b=0����a3+b3=0��������ȷ�ĸ����У�������
A. 1�� B. 2�� C. 3�� D. 4��
B ���������������������Ϊa��ʾ������������a��0����a��0�����ԣ���a����һ��Ϊ����������Ҳ�п���Ϊ�Ǹ����������ʱ����������� �ڸ����ݵij˷����㷨����a��2=a2���ʱ���������ȷ�� �۸������⣬��a=1��b=��4����ô|a|��b����a2��b2�����������ʱ����������� ���������֪a=��b������a3+b3=����b��3+b3=0���ʱ���������ȷ�� ���Ԣڢ���...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡ����������2017-2018ѧ�����꼶���ϣ�������ѧ�Ծ� ���ͣ���ѡ��
���и��������У���ȷ��һ�����ǣ�������
A. 0.28��0.280 B. 0.70��0.07
C. 5������500�� D. 1.1��103��1100
B �����������������A��0.28��ȷ���ٷ�λ��0.280��ȷ��ǧ��λ������Aѡ����� B��0.70��ȷ���ٷ�λ��0.07��ȷ���ٷ�λ������Bѡ����ȷ�� C��5����ȷ������λ��500��ȷ����λ������Cѡ����� D��1.1��103��ȷ����λ��1100��ȷ����λ������Dѡ����� ��ѡB���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�������������ص�һѧ��2017-2018ѧ����꼶���ϣ�������ѧ�Ծ� ���ͣ������
���ʽ���̣�
��1��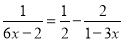
��2��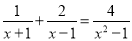 ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�������������ص�һѧ��2017-2018ѧ����꼶���ϣ�������ѧ�Ծ� ���ͣ������
��ʽ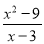 ��_____ʱ��ʽ��ֵΪ�㣬��_____ʱ����ʽ
��_____ʱ��ʽ��ֵΪ�㣬��_____ʱ����ʽ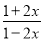 �����壮
�����壮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ��������У2018����꼶���ϣ�������ѧ�Ծ� ���ͣ������
��10�֣���֪����ͼ�٣����ı���ABCD�У�AB��CD����B=90�㣬��P��BC���ϣ�����APD=90��ʱ����֤��ABP�ס�PCD���Ӷ��õ�BP•PC=AB•CD������֤����
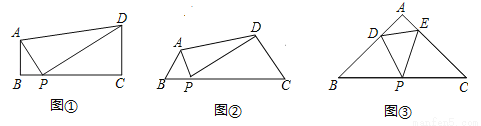
̽������ͼ�ڣ����ı���ABCD�У���P��BC���ϣ�����B=��C=��APDʱ������BP•PC=AB•CD�Գ�������˵�����ɣ�
��չ����ͼ�ۣ��ڡ�ABC�У���P��BC���е㣬��D��E�ֱ��ڱ�AB��AC�ϣ�����B=��C=��DPE=45�㣬BC=4  ��CE=3����DE�ij�Ϊ������
��CE=3����DE�ij�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ���һѧ�������а��꼶��ѧ��ĩ��ϰ�ۺϼ��� ���ͣ���ѡ��
��֪�����١�����ֱ���ϣ���������ͼ���ã��������١��ڵ�����ֱ�Ϊ81 cm2��144 cm2���������۵ı߳�Ϊ��������
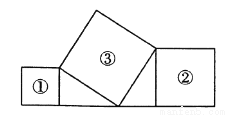
A. 225 cm B. 63 cm C. 50 cm D. 15 cm
D ��������������������ı��١��ڡ��۶��������Σ� ���EAB=��EBD=��BCD=90�㣬BE=BD�� ���AEB+��ABE=90�㣬��ABE+��DBC=90�㣬 ���AEB=��CBD�� �ڡ�ABE�͡�CDB�У� �� ���ABE�ա�CDB��AAS���� ��AE=BC��AB=CD�� �������١��ڵ�����ֱ�81cm2��144cm2�� ��AE2=81��CD2=144�� ��A...�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com