
如图,在△ABC中,BC=3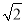 ,AC=5,∠B=45°,则下面结论正确的是_____.
,AC=5,∠B=45°,则下面结论正确的是_____.
①∠C一定是钝角;
②△ABC的外接圆半径为3;
③sinA=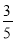 ;
;
④△ABC外接圆的外切正六边形的边长是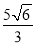 .
.
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:广东省江门市江海区五校2018届九年级上学期期末联考数学试卷 题型:单选题
小玲在一次班会中参与知识抢答活动,现有语文题6个,数学题5个,英语题9个,她从中随机抽取1个,抽中数学题的概率是( )
A. 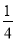 B.
B. 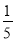 C.
C. 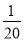 D.
D. 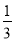
查看答案和解析>>
科目:初中数学 来源:北京市顺义区2018届初三上学期期末考试数学试卷 题型:填空题
在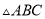 中,
中, 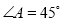 ,
, 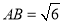 ,
, 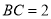 ,则AC的长为__________.
,则AC的长为__________.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年陕西安市九年级(上)期末数学试卷 题型:解答题
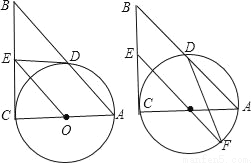
如图,在Rt△ABC中,∠C=90°,以AC为直径作⊙O,交AB于D,过点O作OE∥AB,交BC于E.
(1)求证:ED为⊙O的切线;
(2)如果⊙O的半径为 ,ED=2,延长EO交⊙O于F,连接DF、AF,求△ADF的面积.
,ED=2,延长EO交⊙O于F,连接DF、AF,求△ADF的面积.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年陕西安市九年级(上)期末数学试卷 题型:解答题
解方程:
①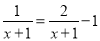 的解x= .
的解x= .
②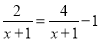 的解x= .
的解x= .
③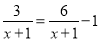 的解x= .
的解x= .
④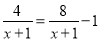 的解x= .
的解x= .
…
(1)根据你发现的规律直接写出⑤,⑥个方程及它们的解.
(2)请你用一个含正整数n的式子表示上述规律,并求出它的解.
①x=0②x=1③x=2④x=3(1)x=4,x=5(2)x=n﹣1 【解析】试题分析:(1)等号左边的分母都是,第一个式子的分子是1,第二个式子的分子是2,那么第5个式子的分子是5,第6个式子的分子是6.等号右边被减数的分母是,分子的等号左边的分子的2倍,减数是1,第一个式子的解是,第二个式子的解是,那么第5个式子的解是第6个式子的解是. (2)由(1)得第个式子的等号左边的分母是,分子...查看答案和解析>>
科目:初中数学 来源:2017-2018学年陕西安市九年级(上)期末数学试卷 题型:单选题
将一个各面涂有颜色的正方体,分割成同样大小的27个小正方体,从这些正方体中任取一个,恰有3个面涂有颜色的概率是( )
A. 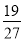 B. 9
B. 9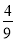 C.
C. 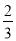 D.
D. 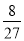
查看答案和解析>>
科目:初中数学 来源:北京市燕山区2018届初三第一学期期末数学试卷 题型:解答题
在平面直角坐标系xOy中,过⊙C上一点P作⊙C的切线l.当入射光线照射在点P处时,产生反射,且满足:反射光线与切线l的夹角和入射光线与切线l的夹角相等,点P称为反射点.规定:光线不能“穿过”⊙C,即当入射光线在⊙C外时,只在圆外进行反射;当入射光线在⊙C内时,只在圆内进行反射.特别地,圆的切线不能作为入射光线和反射光线.光线在⊙C外反射的示意图如图1所示,其中∠1=∠2.
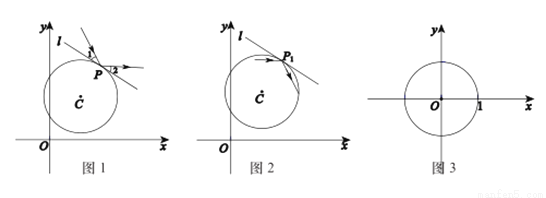
(1)自⊙C内一点出发的入射光线经⊙C第一次反射后的示意图如图2所示,P1是第1个反射点.请在图2中作出光线经⊙C第二次反射后的反射光线和反射点P3;
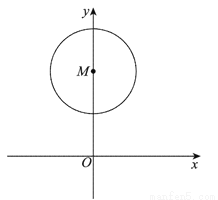
(2)当⊙O的半径为1时,如图3:
①第一象限内的一条入射光线平行于y轴,且自⊙O的外部照射在圆上点P处,此光线经⊙O反射后,反射光线与x轴平行,则反射光线与切线l的夹角为___________°;
②自点M(0,1)出发的入射光线,在⊙O内顺时针方向不断地反射.若第1个反射点是P1,第二个反射点是P2,以此类推,第8个反射点是P8恰好与点M重合,则第1个反射点P1的坐标为___________;
(3)如图4,点M的坐标为(0,2),⊙M的半径为1.第一象限内自点O出发的入射光线经⊙M反射后,反射光线与坐标轴无公共点,求反射点P的纵坐标的取值范围.
查看答案和解析>>
科目:初中数学 来源:北京市2017-2018学年第一学期八年级数学期中试卷 题型:填空题
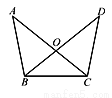
如图,AC、BD相交于点O,∠A=∠D,请补充一个条件,使△AOB≌△DOC,你补充的条件是_____________________(填出一个即可).
查看答案和解析>>
科目:初中数学 来源:福建省2016-2017学年八年级下学期期末考试数学试卷 题型:解答题
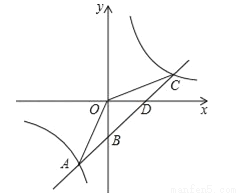
如图,一次函数y=kx+b的图象与反比例函数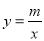 的图象交于点A﹙﹣2,﹣5﹚C﹙5,n﹚,交y轴于点B,交x轴于点D.
的图象交于点A﹙﹣2,﹣5﹚C﹙5,n﹚,交y轴于点B,交x轴于点D.
(1)求反比例函数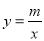 和一次函数y=kx+b的表达式;
和一次函数y=kx+b的表达式;
(2)连接OA,OC.求△AOC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com