
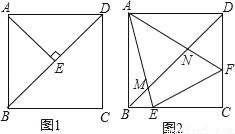
在正方形ABCD中,连接BD.
(1)如图1,AE⊥BD于E.直接写出∠BAE的度数.
(2)如图1,在(1)的条件下,将△AEB以A旋转中心,沿逆时针方向旋转30°后得到△AB′E′,AB′与BD交于M,AE′的延长线与BD交于N.
①依题意补全图1;
②用等式表示线段BM、DN和MN之间的数量关系,并证明.
(3)如图2,E、F是边BC、CD上的点,△CEF周长是正方形ABCD周长的一半,AE、AF分别与BD交于M、N,写出判断线段BM、DN、MN之间数量关系的思路.(不必写出完整推理过程)
科目:初中数学 来源:山东省2018届九年级上期末复习检测数学试卷 题型:解答题
如图,一次函数y=mx+4的图象与x轴相交于点A,与反比例函数y=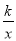 (x>0)的图象相交于点B(1,6).
(x>0)的图象相交于点B(1,6).
(1)求一次函数和反比例函数的解析式;
(2)设点P是x轴上一点,若S△APB=18,直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源:河北省唐山市路南区2017年中考数学三模试卷(解析版) 题型:单选题
如图,已知直线MN∥AB,把△ABC剪成三部分,点C在直线AB上,点O在直线MN上,则点O是△ABC的( )

A. 垂心 B. 重心 C. 内心 D. 外心
C 【解析】试题分析:根据题意可知:点O到AB、AC和BC的距离相等,则点O为三角形三个内角角平分线的交点,即点O为△ABC的内心,故选C.查看答案和解析>>
科目:初中数学 来源:青海省2018届九年级上学期12月月考数学试卷 题型:填空题
将矩形纸片ABCD(如图)那样折起,使顶点C落在C?处,测量得AB=4,DE=8,则sin∠C?ED为________________.
查看答案和解析>>
科目:初中数学 来源:青海省2018届九年级上学期12月月考数学试卷 题型:单选题
在Rt△ABC中,∠C=90°,sinA=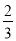 ,那么tanB的值是( )
,那么tanB的值是( )
A. 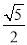 B.
B. 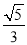 C.
C. 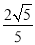 D.
D. 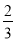
查看答案和解析>>
科目:初中数学 来源:2017年湖南省郴州市临武县景山学校中考数学模拟试卷 题型:解答题
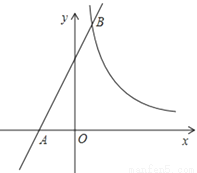
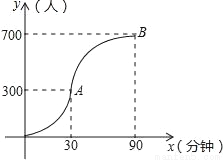
科技馆是少年儿童节假日游玩的乐园.
如图所示,图中点的横坐标x表示科技馆从8:30开门后经过的时间(分钟),纵坐标y表示到达科技馆的总人数.图中曲线对应的函数解析式为y=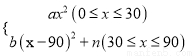 ,10:00之后来的游客较少可忽略不计.
,10:00之后来的游客较少可忽略不计.
(1)请写出图中曲线对应的函数解析式;
(2)为保证科技馆内游客的游玩质量,馆内人数不超过684人,后来的人在馆外休息区等待.从10:30开始到12:00馆内陆续有人离馆,平均每分钟离馆4人,直到馆内人数减少到624人时,馆外等待的游客可全部进入.请问馆外游客最多等待多少分钟?
查看答案和解析>>
科目:初中数学 来源:2017年湖南省郴州市临武县景山学校中考数学模拟试卷 题型:填空题
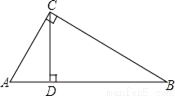
如图在Rt△ABC中,∠C=90°.CD是斜边AB上的高,若得到CD2=BD•AD这个结论可证明_____∽_____.
查看答案和解析>>
科目:初中数学 来源:山东省潍坊高新技术产业开发区2017-2018学年七年级上期末模拟数学试卷 题型:解答题
如图,是一个正六棱柱,它的底面边长是3cm,高是6cm.
(1)这个棱柱的侧面积是多少?
(2)这个棱柱共有多少条棱?所有的棱长的和是多少?
(3)这个棱柱共有多少个顶点?
(4)通过观察,试用含n的式子表示n棱柱的面数与棱的条数.
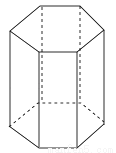
查看答案和解析>>
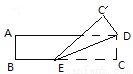
科目:初中数学 来源:2017年湖北省黄石市中考数学模拟试卷 题型:解答题
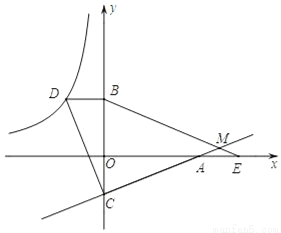
如图,已知点D在反比例函数y=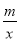 的图象上,过点D作x轴的平行线交y轴于点B(0,3),过点A(5,0)的直线y=kx+b与y轴于点C,且BD=OC,tan∠OAC=
的图象上,过点D作x轴的平行线交y轴于点B(0,3),过点A(5,0)的直线y=kx+b与y轴于点C,且BD=OC,tan∠OAC=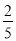 .
.
(1)求反比例函数y=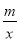 和直线y=kx+b的解析式;
和直线y=kx+b的解析式;
(2)连接CD,试判断线段AC与线段CD的关系,并说明理由;
(3)点E为x轴上点A右侧的一点,且AE=OC,连接BE交直线CA于点M,求∠BMC的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com