练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    下列图形中，∠1和∠2是同位角的有 ( )

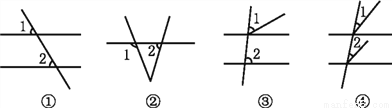
    A. 1个 B. 2个 C. 3个 D. 4个

    D 【解析】根据两条直线被第三条直线所截，位于截线的同侧，被截线的同旁的两角为同位角，可知①②③④中的∠1、∠2均为同位角. 故选：D.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：北师大版七年级下册 2.2 探索直线平行的条件（1） 同步练习 题型：单选题

    某人在广场上练习驾驶汽车，两次拐弯后，行驶方向与原来相同，这两次拐弯的角度可能是（ ）

    A. 第一次左拐30°，第二次右拐30°

    B. 第一次右拐50°，第二次左拐130°

    C. 第一次右拐50°，第二次右拐130°

    D. 第一次向左拐50°，第二次向左拐120°

    A 【解析】试题解析：如图： 故选：A．

    查看答案和解析>>

    科目：初中数学 来源：人教版2017-2018学年九年级下册数学全册综合测试卷 题型：填空题

    已知，则=________．

    7 【解析】设===k≠0， 所以，a=2k，b=3k，c=4k， 所以, ===7， 故答案为：7.

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下2.2.1 用“同位角、第三直线”判定平行线 同步练习 题型：解答题

    如图,已知直线a,b,c,d,e,且∠1=∠2,∠3=∠4,则a与c平行吗?为什么?

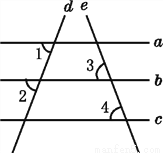
    解:a与c平行.

    理由:因为∠1=∠2(_________________), 

    所以a∥b(_________________). 

    因为∠3=∠4(_________________), 

    所以b∥c(_________________). 

    所以a∥c(_________________).

    已知;同位角相等,两直线平行;已知;同位角相等,两直线平行;平行于同一条直线的两条直线平行 【解析】由已知∠1=∠2，根据内错角相等，两直线平行可知a∥b，由∠3=∠4，根据同旁内角互补，两直线平行可知b∥c，根据如果两条直线都与第三条直线平行那么这两条直线平行得出结论a∥c． 故答案为：已知;同位角相等,两直线平行;已知;同位角相等,两直线平行;平行于同一条直线的两条直线平行.

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下2.2.1 用“同位角、第三直线”判定平行线 同步练习 题型：单选题

    下列说法正确的是(　　)

    A. 两条不相交的直线叫做平行线

    B. 过一点有且只有一条直线与已知直线平行

    C. 在同一平面内不相交的两条线段互相平行

    D. 在同一平面内不相交的两条直线叫做平行线

    D 【解析】根据同一平面内，不相交的直线互相平行，两条线段或射线平行是指它们所在的直线平行，依次判断各项即可知：

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年九年级数学北师大版上册 全册综合测试卷1 题型：解答题

    已知：如图，在△ABC中，AB=AC，AD⊥BC，垂足为点D，AN是△ABC外角∠CAM的平分线，CE⊥AN，垂足为点E，

    （1）求证：四边形ADCE为矩形；

    （2）当△ABC满足什么条件时，四边形ADCE是一个正方形？并给出证明．

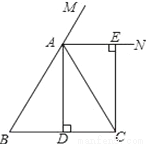
    （1）证明见解析；（2）当△ABC满足∠BAC=90°时，四边形ADCE是一个正方形，理由见解析. 【解析】试题分析：（1）求出∠BAD=∠DAC，∠MAE=∠CAE，求出∠DAE的度数，求出∠AEC=∠ADC=∠EAD=90°，根据矩形的判定判断即可； （2）求出AD=DC，得出∠ACD=∠DAC=45°，求出∠BAC=90°，即可求出答案． 试题解析：（1）证明：∵在△ABC...

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年九年级数学北师大版上册 全册综合测试卷1 题型：填空题

    如图，一条河的两岸有一段是平行的，在河的南岸边每隔5米有一棵树，在北岸边每隔50米有一根电线杆，小丽站在离岸边15米的点P处看北岸，发现北岸相邻的两根电线杆恰好被南岸的两棵树遮住，并且这两棵树之间还有三棵树，则河的宽度为_______米．

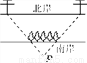
    22.5 【解析】试题分析：根据题意，河两岸平行，故可根据平行线分线段成比例来解决问题，列出方程，求解即可． 【解析】 如图，设河宽为h， ∵AB∥CD 由平行线分线段成比例定理得：=， 解得：h=22.5， ∴河宽为22.5米． 故答案为：22.5．

    查看答案和解析>>

    科目：初中数学 来源：江苏省张家港市2017-2018学年第一学期初三数学期末考试试卷 题型：解答题

    如图，已知一条直线过点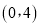，且与抛物线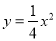交于A、B两点，其中点A的横坐标是-2.

    ⑴求这条直线的函数关系式及点B的坐标 ；

    ⑵在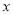轴上是否存在点C,使得?ABC是直角三角形？若存在，求出点C的坐标，若不存在，请说明理由；

    ⑶.过线段AB上一点P,作PM∥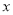轴，交抛物线于点M,点M在第一象限；点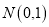，当点M的横坐标为何值时，MN+3MP的长度最大？最大值是多少？

    （1）点B的坐标为（8，16）；（2）点C的坐标为（，0），（0，0），（6，0），（32，0）；（3）当M的横坐标为6时，MN+3PM的长度的最大值是18. 【解析】试题分析：(1)、根据点A在二次函数上求出点A的坐标，然后利用待定系数法求出一次函数的解析式，根据一次函数和二次函数的交点坐标求出求出点B的坐标；(2)、根据点A和点B的坐标求出的值，设点C的坐标为(m，0)，然后分别求出和的...

    查看答案和解析>>

    科目：初中数学 来源：2018人教版九年级数学下册练习：期中检测卷 题型：填空题

    若函数y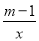＝的图象在同一象限内，y随x增大而增大，则m的值可以是_____．(写出一个即可)

    0(答案不唯一，只要满足m＜1即可) 【解析】试题分析：根据反比例函数图象的性质得到m-1＜0，通过解该不等式可以求得m的取值范围，据此可以取一个m值． 试题解析：∵函数的图象在同一象限内，y随x增大而增大， ∴m-1＜0， 解得 m＜1． 故m可以取0，-1，-2等值．

    查看答案和解析>>

    同步练习册答案