练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，已知一条直线过点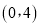，且与抛物线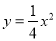交于A、B两点，其中点A的横坐标是-2.

    ⑴求这条直线的函数关系式及点B的坐标 ；

    ⑵在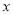轴上是否存在点C,使得?ABC是直角三角形？若存在，求出点C的坐标，若不存在，请说明理由；

    ⑶.过线段AB上一点P,作PM∥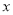轴，交抛物线于点M,点M在第一象限；点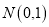，当点M的横坐标为何值时，MN+3MP的长度最大？最大值是多少？

    （1）点B的坐标为（8，16）；（2）点C的坐标为（，0），（0，0），（6，0），（32，0）；（3）当M的横坐标为6时，MN+3PM的长度的最大值是18. 【解析】试题分析：(1)、根据点A在二次函数上求出点A的坐标，然后利用待定系数法求出一次函数的解析式，根据一次函数和二次函数的交点坐标求出求出点B的坐标；(2)、根据点A和点B的坐标求出的值，设点C的坐标为(m，0)，然后分别求出和的...
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：人教版2017-2018学年九年级下册数学全册综合测试卷 题型：解答题

    如图，某大楼的顶部有一块广告牌CD，小李在山坡的坡脚A处测得广告牌底部D的仰角为60°．沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°，已知sin∠BAH=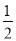，AB=10米，AE=15米．

    （1）求点B距水平面AE的高度BH；

    （2）求广告牌CD的高度．

    （1）5米；（2）广告牌CD的高度为（20﹣10）米． 【解析】试题分析：（1）根据正弦的概念求出BH的长； （2）在△ADE解直角三角形求出DE的长，进而可求出EH即BG的长，在Rt△CBG中，∠CBG=45°，则CG=BG，由此可求出CG的长然后根据CD=CG+GE-DE即可求出广告牌的高度． 试题解析：（1）由题意得，sin∠BAH=，又AB=10米， ∴BH= AB...

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下2.2.1 用“同位角、第三直线”判定平行线 同步练习 题型：单选题

    下列图形中，∠1和∠2是同位角的有 ( )

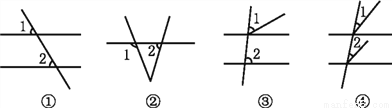
    A. 1个 B. 2个 C. 3个 D. 4个

    D 【解析】根据两条直线被第三条直线所截，位于截线的同侧，被截线的同旁的两角为同位角，可知①②③④中的∠1、∠2均为同位角. 故选：D.

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年九年级数学北师大版上册 全册综合测试卷1 题型：填空题

    若两个相似三角形的周长比为2：3，则它们的面积比是_________.

    4∶9 【解析】试题解析：∵两个相似三角形的周长比为2：3， ∴这两个相似三角形的相似比为2：3， ∴它们的面积比是4：9．

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年九年级数学北师大版上册 全册综合测试卷1 题型：单选题

    反比例函数y=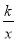的图象与函数y=2x的图象没有交点，若点(－2，y1)，(－1，y2)，(1，y3)在这个反比例函数y=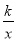的图象上，则下列结论中正确的是（ ）

    A. y1＞y2＞y3 B. y2＞y1＞y3C．y3＞y1＞y2 D．y3＞y2＞y1

    B 【解析】因为反比例函数y=的图象与函数y=2x的图象没有交点,所以反比例函数y=的图象分布在二,四象限,根据反比例函数的图象性质画出反比例函数图象,观察图象可得:y2＞y1＞y3,故选B.

    查看答案和解析>>

    科目：初中数学 来源：江苏省张家港市2017-2018学年第一学期初三数学期末考试试卷 题型：解答题

    南沙群岛是我国固有领土，现在我南海渔民要在南沙某海岛附近进行捕鱼作业，当渔船航行至B处时，测得该岛位于正北方向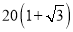海里的C处，为了防止某国还巡警干扰，就请求我A处的鱼监船前往C处护航，已知C位于A处的北偏东45°方向上，A位于B的北偏西30°的方向上，求A、C之间的距离．

    ． 【解析】试题分析：作AD⊥BC，垂足为D，设CD=x，利用解直角三角形的知识，可得出AD，继而可得出BD，结合题意BC=CD+BD可得出方程，解出x的值后即可得出答案． 试题解析：如图，作AD⊥BC，垂足为D， 由题意得，∠ACD=45°，∠ABD=30°． 设CD=x，在Rt△ACD中，可得AD=x， 在Rt△ABD中，可得BD= ， 又∵BC=20（1+...

    查看答案和解析>>

    科目：初中数学 来源：江苏省张家港市2017-2018学年第一学期初三数学期末考试试卷 题型：填空题

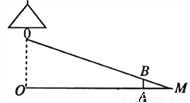
    如图，电线杆上的路灯距离地面8米，身高1. 6米的小明(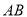)站在距离电线杆的底部(点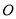)20米的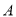处，则小明的影子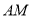长为________米.

    5 【解析】试题解析：由题意得, 即 解得：AM=5. 故答案为：5.

    查看答案和解析>>

    科目：初中数学 来源：2018人教版九年级数学下册练习：期中检测卷 题型：解答题

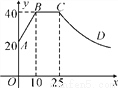
    心理学家研究发现，一般情况下，一节课40分钟中，学生的注意力随教师讲课的变化而变化．开始上课时，学生的注意力逐步增强，中间有一段时间学生的注意力保持较为理想的稳定状态，随后学生的注意力开始分散．经过实验分析可知， 学生的注意力指标数y随时间x(分钟)的变化规律如图所示(其中AB，BC分别为线段，CD为双曲线的一部分)．

    (1)开始上课后第5分钟时与第30分钟时相比较，何时学生的注意力更集中？

    (2)一道数学竞赛题，需要讲19分钟，为了效果较好，要求学生的注意力指标数最低达到36，那么经过适当安排，老师能否在学生注意力达到所需的状态下讲解完这道题目？

    （1）第30分钟注意力更集中；（2）老师能在学生注意力达到所需的状态下讲解完成这道题目，理由见解析. 【解析】试题分析：（1）先用代定系数法分别求出AB和CD的函数表达式，再分别求第五分钟和第三十分钟的注意力指数，最后比较判断. （2）分别求出注意力指数为36时的两个时间，再将两时间之差和19比较，大于19则能讲完，否则不能． 试题解析： (1)由题意得y1＝2x＋20(0...

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级下册数学 第二章 相交线与平行线 单元检测卷 题型：单选题

    如图，若∠1=50°，∠C=50°，∠2=120°，则( )

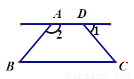
    A.∠B =40° B.∠B=50° C.∠B=60° D.∠B=120°

    C． 【解析】 试题解析：∵∠1=50°，∠C=50°， ∴AD∥BC， ∴∠2与∠B互补． ∵∠2=120°， ∴∠B=180°-120°=60°． 故选C．

    查看答案和解析>>

    同步练习册答案