
一个几何体的三视图如图所示,则该几何体可能是( )
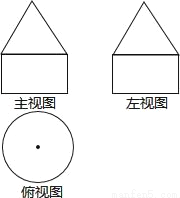
A. 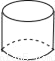 B.
B. 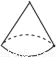 C.
C. 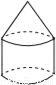 D.
D. 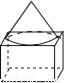
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案科目:初中数学 来源:江苏省2018届九年级上学期期末模拟数学试卷 题型:解答题
为给人们的生活带来方便,2017年兴化市准备在部分城区实施公共自行车免费服务.图1是公共自行车的实物图,图2是公共自行车的车架示意图,点A、D、C、E在同一条直线上,CD=35cm,DF=24cm,AF=30cm,FD⊥AE于点D,座杆CE=15cm,且∠EAB=75°.
(1)求AD的长;
(2)求点E到AB的距离(结果保留整数).
(参考数据:sin75°≈0.97,cos75°≈0.26,tan75°≈3.73)

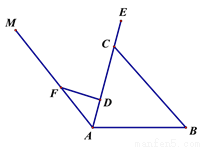
图 1 图2
(1)AD=18;(2)车座点E到车架档AB的距离约是66cm. 【解析】(1)在Rt△ADF中,利用勾股定理可求出AD的长;(2)先考虑作辅助线,过点E作EH⊥AB,垂足为H,利用∠EAH的正弦列式求EH的长即可. 【解析】 (1)在Rt△ADF中,AF=30,DF=24, 由勾股定理得:AD==18cm; (2)过点E作EH⊥AB,垂足为H, ∵AE=AD+DC...查看答案和解析>>
科目:初中数学 来源:山东省临朐县沂山风景区2017-2018学年七年级上期末模拟数学试卷 题型:单选题
如果鸭绿江水位高1m时水位变化记作+1m,那么水位下降0.5m时水位变化记作( )
A. ﹣0.5m B. 0.5m C. 1.5m D. ﹣1.5m
A 【解析】∵水位升高1m时水位变化记作+1m, ∴水位下降0.5 m时水位变化记作﹣0.5m, 故选A.查看答案和解析>>
科目:初中数学 来源:2017年湖南省郴州市中考数学模拟试卷 题型:填空题
如图,△ABC中,AC=6,AB=4,点D与点A在直线BC的同侧,且∠ACD=∠ABC,CD=2,点E是线段BC延长线上的动点,当△DCE和△ABC相似时,线段CE的长为_____.

查看答案和解析>>
科目:初中数学 来源:2017年湖南省郴州市中考数学模拟试卷 题型:单选题
如图,在矩形ABCD中,AD=6,AB=4,点E、G、H、F分别在AB、BC、CD、AD上,且AF=CG=2,BE=DH=1,点P是直线EF、GH之间任意一点,连接PE、PF、PG、PH,则图中阴影面积(△PEF和△PGH的面积和)等于( )
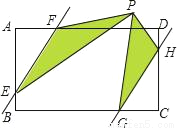
A. 7 B. 8 C. 12 D. 14
A 【解析】连接EG,FH, ∵在矩形ABCD中,AD=6,AB=4,AF=CG=2,BE=DH=1, ∴AE=AB?BE=4?1=3, CH=CD?DH=4?1=3, ∴AE=CH, 在△AEF与△CGH中, , ∴△AEF≌△CGH(SAS), ∴EF=GH, 同理可得,△BGE≌△DFH, ∴EG=FH, ∴四边形EGH...查看答案和解析>>
科目:初中数学 来源:2017年湖北省中考数学模拟试卷 题型:解答题
在平面直角坐标系中,点 A(﹣2,0),B(2,0),C(0,2),点 D,点E分别是 AC,BC的中点,将△CDE绕点C逆时针旋转得到△CD′E′,及旋转角为α,连接 AD′,BE′.
(1)如图①,若 0°<α<90°,当 AD′∥CE′时,求α的大小;
(2)如图②,若 90°<α<180°,当点 D′落在线段 BE′上时,求 sin∠CBE′的值;
(3)若直线AD′与直线BE′相交于点P,求点P的横坐标m的取值范围(直接写出结果即可).
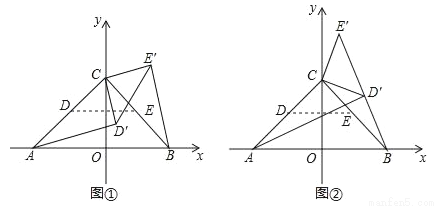
查看答案和解析>>
科目:初中数学 来源:2017年湖北省中考数学模拟试卷 题型:填空题
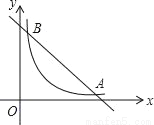
如图,在直角坐标系中,直线y=6﹣x与双曲线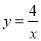 (x>0)的图象相交于A、B,设点A的坐标为(m,n),那么以m为长,n为宽的矩形的面积和周长分别为_____,_____.
(x>0)的图象相交于A、B,设点A的坐标为(m,n),那么以m为长,n为宽的矩形的面积和周长分别为_____,_____.
查看答案和解析>>
科目:初中数学 来源:山东省2017-2018学年八年级上期末模拟数学试卷 题型:解答题
如图,已知E,F是线段AB上的两点,且AE=BF,AD=BC,∠A=∠B.求证:DF=CE.

查看答案和解析>>
科目:初中数学 来源:吉林省长春汽车经济技术开发区2017-2018学年八年级上学期期末教学质量跟踪测试数学试卷 题型:单选题
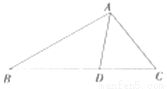
如图,AD是△ABC的角平分线,且AB:AC=3:2,则△ABD与△ACD的面积之比为( )
A. 3:2 B. 4:6 C. 9:4 D. 不能确定
A 【解析】试题解析:过点D作DE⊥AB于E,DF⊥AC于F. ∵AD为∠BAC的平分线, ∴DE=DF,又AB:AC=3:2, ∴S△ABD:S△ACD=(AB•DE):(AC•DF)=AB:AC=3:2. 故选A.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com