
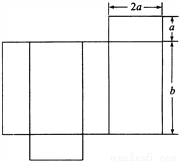
如图是一个食品包装盒的表面展开图.
(1)请写出包装盒的几何体名称;
(2)根据图中所标尺寸,用a,b表示这个几何体的全面积S(侧面积与底面积之和),并计算当a=1,b=4时,S的值.
科目:初中数学 来源:贵州省黔南州2017-2018学年八年级上学期期末联考数学试卷 题型:解答题
计算:
(1) 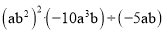 (2)
(2) 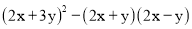
查看答案和解析>>
科目:初中数学 来源:新疆乌鲁木齐市2018届九年级上学期期末考试数学试卷 题型:单选题
将一枚质地均匀的骰子掷两次,则两次点数之和等于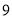 的概率为( )
的概率为( )
A. 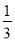 B.
B. 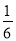 C.
C. 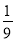 D.
D. 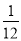
查看答案和解析>>
科目:初中数学 来源:河南省商丘市2017-2018学年上期七年级数学期末第一次模拟检测试卷 题型:解答题
点O为直线AB上一点,过点O作射线OC,使∠BOC=65°,将一直角三角形的直角三角板的直角顶点放在点O处.
(1)如图1,将三角板MON的一边ON与射线OB重合,则∠MOC=___________;
(2)如图2,将三角板MON绕点O逆时针旋转一定角度,此时OC是∠MOB的角平分线,求旋转角∠BON和∠CON的度数;
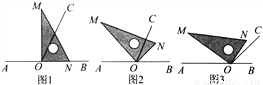
(3)将三角板MON绕点O逆时针旋转至图3时,∠NOC= ∠AOM,求∠NOB的度数.
∠AOM,求∠NOB的度数.
查看答案和解析>>
科目:初中数学 来源:河南省商丘市2017-2018学年上期七年级数学期末第一次模拟检测试卷 题型:单选题
如图,是直角顶点重合的一副三角尺,若∠BCD=30°,下列结论错误的是( )
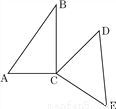
A. ∠ACD=120° B. ∠ACD=∠BCE C. ∠ACE=120° D. ∠ACE-∠BCD=120°
C 【解析】根据题意,可知∠ACB=∠DCE=90°,然后由∠BCD=30°,可得∠ACD=∠BCE=120°,而∠ACE=360°-120°-90°=150°,因此可求得∠ACE-∠BCD=150°-30°=120°. 故选:C.查看答案和解析>>
科目:初中数学 来源:河南省商丘市2017-2018学年上期七年级数学期末第一次模拟检测试卷 题型:填空题
如图,OA的方向是北偏东15°,OB的方向是北偏西40°,若∠AOC=∠AOB,则OC的方向是__
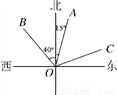
查看答案和解析>>
科目:初中数学 来源:江苏省盐城市盐都区2017届九年级上学期期末考试数学试卷 题型:填空题
某公司今年4月份营业额为60万元,6月份营业额达到100万元,设该公司5、6两个月营业额的月均增长率为x,则可列方程为 .
60(1+x)2=100 【解析】试题分析:设平均每月的增长率为x,根据4月份的营业额为60万元,6月份的营业额为100万元,分别表示出5,6月的营业额,即可列出方程.设平均每月的增长率为x,根据题意可得:60(1+x)2=100查看答案和解析>>
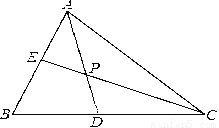
科目:初中数学 来源:河南省2017-2018学年八年级上学期期末考试数学试卷 题型:解答题
如图,△ABC中,∠ABC=60°,AD、CE分别平分∠BAC、∠ACB,AD、CE相交于点P
(1) 求∠CPD的度数
(2) 若AE=3,CD=7,求线段AC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com