
关于x的方程ax2-(3a+1)x+2(a+1)=0有两个不相等的实数根x1,x2,且有x1-x1x2+x2=1-a,则a的值是 ( )
A. 1 B. -1 C. 1或-1 D. 2
B 【解析】由根与系数的关系知,x1+x2=, x1x2=, x1-x1x2+x2=1-a, , , a=, 代入原方程,a=1时,有两个相等的实数根. 所以a=-1. 选B. 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案科目:初中数学 来源:福建省南平市2017-2018学年第一学期七年级期末质量检测数学试卷 题型:单选题
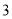 的倒数等于( )
的倒数等于( )
A. 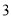 B.
B. 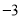 C.
C. 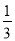 D.
D. 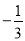
查看答案和解析>>
科目:初中数学 来源:北师大版数学七年级下册第一章整式乘法1.2幂的乘方与积的乘方课时练习 题型:单选题
(2x)3 等于( )
A. -x7 B. x10 C. x9 D. 8x3
D 【解析】试题解析: 故D项正确. 故选D.查看答案和解析>>
科目:初中数学 来源:2017-2018学年九年级数学北师大版上册 第2章 一元二次方程 单元测试卷 题型:填空题
已知x为实数,且满足(x2+3x) 2+(x2+3x)-6=0,则x2+3x的值为___________.
2 【解析】试题解析: 没有实数根. 故答案为:查看答案和解析>>
科目:初中数学 来源:2017-2018学年九年级数学北师大版上册 第2章 一元二次方程 单元测试卷 题型:单选题
方程x2﹣2x+3=0的根的情况是( )
A. 有两个相等的实数根 B. 只有一个实数根
C. 没有实数根 D. 有两个不相等的实数根
C 【解析】试题分析:利用根的判别式进行判断. 【解析】 ∵ ∴此方程无实数根. 故选C.查看答案和解析>>
科目:初中数学 来源:2017-2018学年八年级数学北师大版上册 第1-4章综合测试卷 题型:解答题
如图,圆柱形玻璃容器高19cm,底面周长为60cm,在外侧距下底1.5cm的点A处有一只蜘蛛,在蜘蛛正对面的圆柱形容器的外侧,距上底1.5cm处的点B处有一只苍蝇,蜘蛛急于捕捉苍蝇充饥,请你帮蜘蛛计算它沿容器侧面爬行的最短距离.
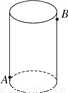
查看答案和解析>>
科目:初中数学 来源:2017-2018学年八年级数学北师大版上册 第1-4章综合测试卷 题型:填空题
如图,在Rt△ABC中,∠BCA=90°,点D是BC上一点,AD=BD,若AB=8,BD=5,则CD=________.
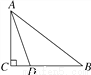
查看答案和解析>>
科目:初中数学 来源:北师大版九年级下册数学全册综合测试卷二 题型:解答题
如图,已知抛物线y=ax2+bx+c(a>0,c<0)交x轴于点A,B,交y轴于点C,设过点A,B,C三点的圆与y轴的另一个交点为D.
(1)如图1,已知点A,B,C的坐标分别为(﹣2,0),(8,0),(0,﹣4);
①求此抛物线的表达式与点D的坐标;
②若点M为抛物线上的一动点,且位于第四象限,求△BDM面积的最大值;
(2)如图2,若a=1,求证:无论b,c取何值,点D均为定点,求出该定点坐标.
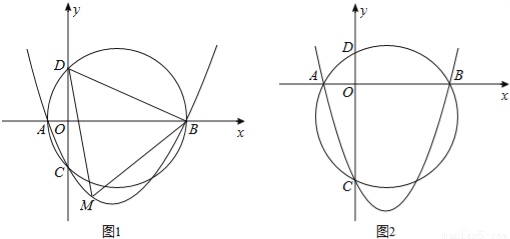
查看答案和解析>>
科目:初中数学 来源:北师大版九年级下册数学全册综合测试卷一 题型:解答题
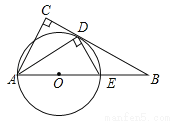
如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,DE⊥AD,交AB于点E,AE为⊙O的直径.
(1)判断BC与⊙O的位置关系,并证明你的结论;
(2)求证:△ABD∽△DBE;
(3)若cosB=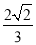 ,AE=4,求CD.
,AE=4,求CD.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com