
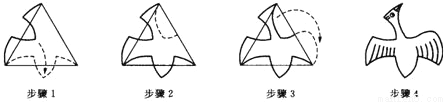
如图,从正三角形出发,利用旋转,作一个飞鸟图.请你也利用正三角形用旋转设计一个图案.

科目:初中数学 来源:人教版九年级上册数学 第24章小结与复习 练习 题型:单选题
在半径为2的圆中,弦AB的长为2,则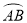 的长等于( )
的长等于( )
A. 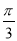 B.
B.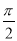 C.
C.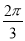 D.
D.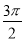
查看答案和解析>>
科目:初中数学 来源:人教版九年级上册数学 24.2.2直线和圆的位置关系(1)练习 题型:解答题
Rt△ABC中,∠C=90°,AC=6,BC=8.求△ABC的内切圆半径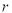 .
.
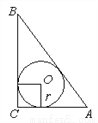
查看答案和解析>>
科目:初中数学 来源:人教版九年级上册数学 21.2.1配方法(1)练习 题型:单选题
x1,x2是一元二次方程3(x-1)2=15的两个解,且x1<x2,下列说法正确的是( )
A. x1小于-1,x2大于3 B. x1小于-2,x2大于3
C. x1,x2在-1和3之间 D. x1,x2都小于3
A 【解析】试题分析:∵x1、x2是一元二次方程3(x﹣1)2=15的两个解,且x1<x2,∴(x﹣1)2=5,∴x﹣1=±,∴x2=1+>3,x1=1﹣<﹣1. 故选:A.查看答案和解析>>
科目:初中数学 来源:人教版九年级上册数学 21.2.1配方法(1)练习 题型:解答题
用直接开平方法解方程:
(1) 9x2=25;
(2) x2-144=0.
(1) x1=,x2=- (2) x1=12,x2=-12 【解析】试题分析: (1)系数化为1后,直接开平方求解; (2)先把常数项移到等号的右边,再用直接开平方法求解. 试题解析: (1) 【解析】 9x2=25,x2=,所以x1=,x2=- (2) 【解析】 x2-144=0,x2=144,所以x1=12,x2=-12.查看答案和解析>>
科目:初中数学 来源:人教版九年级上册数学 23.3课题学习图案设计 测试 题型:单选题
如图可以看作是由正五边形经过几次旋转得到的,则每次旋转的度数为( ).
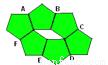
A. 72° B. 90° C. 108° D. 144°
C 【解析】正五边形的内角是180°×(5-2)÷5=108°,所以图形是绕正五边形的顶点,经过6次顺时针旋转108°后得到的. 故选C.查看答案和解析>>
科目:初中数学 来源:人教版九年级上册数学 23.1图形的旋转(2)测试 题型:解答题
如图:若∠AOD=∠BOC=60°,A、O、C三点在同一条线上,△AOB与△COD是能够重合的图形.求:
(1)旋转中心;
(2)旋转角度数;
(3)图中经过旋转后能重合的三角形共有几对?若A、O、C三点不共线,结论还成立吗?为什么?
(4)求当△BOC为等腰直角三角形时的旋转角度;
(5)若∠A=15°,则求当A、C、B在同一条线上时的旋转角度.
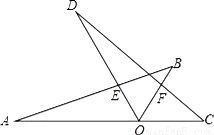
查看答案和解析>>
科目:初中数学 来源:人教版九年级上册数学 24.4弧长和扇形面积(2)练习 题型:单选题
在Rt△ABC中,已知AB=6,AC=8,∠A=90°.如果把Rt△ABC绕直线AC旋转一周得到一个圆锥,其全面积为S1;把Rt△ABC绕直线AB旋转一周得到另一个圆锥,其全面积为S2.那么S1∶S2等于( )
A. 2∶3 B. 3∶4 C. 4∶9 D. 5∶12
A 【解析】试题解析: 绕直线旋转一周得到一个圆锥,全面积 绕直线旋转一周得到一个圆锥,全面积 故选A.查看答案和解析>>
科目:初中数学 来源:人教版九年级上册数学 22.1.4二次函数yax2+bx+c的图象和性质(2)测试 题型:解答题
已知抛物线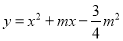 (m>0)与x轴交于A、B两点.
(m>0)与x轴交于A、B两点.
(1)求证:抛物线的对称轴在y轴的左侧;
(2)若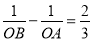 (O为坐标原点),求抛物线的解析式;
(O为坐标原点),求抛物线的解析式;
(3)设抛物线与y轴交于点C,若△ABC是直角三角形.求△ABC的面积.
(1)证明见解析(2)y=x2+2x﹣3(3) 【解析】试题分析:(1)证明抛物线的对称轴<0即可证明抛物线的对称轴在y轴的左侧; (2)根据题中已知条件求出m的值,进而求得抛物线的解析式; (3)先设出C点坐标,根据的x1与x2关系求出m值,进而可求得△ABC的面积. 【解析】 (1)证明:∵m>0, ∴x=﹣=﹣<0, ∴抛物线的对称轴在y轴的左侧; (2)...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com