
在Rt△ABC中,已知AB=6,AC=8,∠A=90°.如果把Rt△ABC绕直线AC旋转一周得到一个圆锥,其全面积为S1;把Rt△ABC绕直线AB旋转一周得到另一个圆锥,其全面积为S2.那么S1∶S2等于( )
A. 2∶3 B. 3∶4 C. 4∶9 D. 5∶12
A 【解析】试题解析: 绕直线旋转一周得到一个圆锥,全面积 绕直线旋转一周得到一个圆锥,全面积 故选A. 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:《概率的进一步认识》单元测试2 题型:单选题
有一对酷爱运动的年轻夫妇给他们12个月大的婴儿拼排3块分别写有”20”,”08”和”北京”的字块,如果婴儿能够排成”2008北京”或者”北京2008”,则他们就给婴儿奖励.假设婴儿能将字块横着正排,那么这个婴儿能得到奖励的概率是 ( )
A.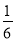 B.
B.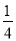 C.
C.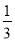 D.
D.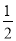
查看答案和解析>>
科目:初中数学 来源:人教版九年级上册数学 23.3课题学习图案设计 测试 题型:解答题
如图,从正三角形出发,利用旋转,作一个飞鸟图.请你也利用正三角形用旋转设计一个图案.
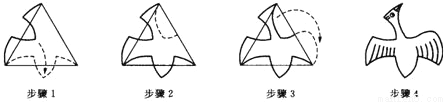

查看答案和解析>>
科目:初中数学 来源:人教版九年级上册数学 23.1图形的旋转(2)测试 题型:填空题
如图,将△OAB绕点O按逆时针方面旋转至△0A′B′,使点B恰好落在边A′B′上.已知AB=4cm,BB′=1cm,则A′B长是______cm.
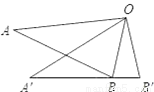
查看答案和解析>>
科目:初中数学 来源:人教版九年级上册数学 23.1图形的旋转(2)测试 题型:单选题
在图形旋转中,下列说法错误的是( )
A. 图形上的每一点到旋转中心的距离相等 B. 图形上的每一点转动的角度相同
C. 图形上可能存在不动点 D. 图形上任意两点的连线与其对应两点的连线相等
A 【解析】A选项,在图形旋转中,根据旋转的性质,图形上对应点到旋转中心的距离相等,故A选项错误, B选项,图形上的每一点转动的角度都等于旋转角,故B选项正确, C选项,图形上一点为旋转中心,则这个点不动, 故C选项正确, D选项,旋转前后两个图形全等,则图形上任意两点的连线与其对应两点的连线相等, 故D选项正确, 故选A.查看答案和解析>>
科目:初中数学 来源:人教版九年级上册数学 24.4弧长和扇形面积(2)练习 题型:填空题
如图,已知圆锥的母线长OA=8,地面圆的半径r=2.若一只小虫从A点出发,绕圆锥的侧面爬行一周后又回到A点,则小虫爬行的最短路线的长是_________(结果保留根式).
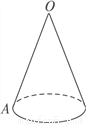
查看答案和解析>>
科目:初中数学 来源:人教版九年级上册数学 24.4弧长和扇形面积(2)练习 题型:填空题
圆锥的底面积为25π,母线长为13 cm,这个圆锥的底面圆的半径为________ cm,高为________ cm,侧面积为________ cm2.
5;12; 65π. 【解析】设底面半径是r,高是h ∵s= , 25π= , r=5. h=, 底面周长是10, .查看答案和解析>>
科目:初中数学 来源:《概率的进一步认识》单元测试4 题型:填空题
如图,每一个标有数字的方块均是可以翻动的木牌,其中只有两块木牌的背面贴有中奖标志,则随机翻动一块木牌中奖的概率为_______.
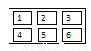
查看答案和解析>>
科目:初中数学 来源:天津市 2017-2018学年 八年级数学上册 全等三角形判定 填空题练习(含答案) 题型:填空题
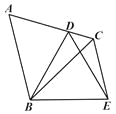
如图,△ABC是等边三角形,点D为 AC边上一点,以BD为边作等边△BDE, 连接CE.若CD=1,CE=3,则BC=_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com