练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

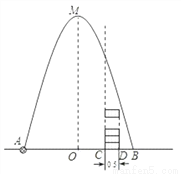
    如图，在水平地面点A处有一网球发射器向空中发射网球，网球飞行路线是一条抛物线，在地面上落点为B，有人在直线AB上点C（靠点B一侧）竖直向上摆放若干个无盖的圆柱形桶．试图让网球落入桶内，已知AB=4米，AC=3米，网球飞行最大高度OM=5米，圆柱形桶的直径为0.5米，高为0.3米（网球的体积和圆柱形桶的厚度忽略不计）．当竖直摆放圆柱形桶至少________ 个时，网球可以落入桶内．

    8 【解析】以点O为原点，AB所在直线为x轴建立直角坐标系（如图）， M（0，5），B（2，0），C（1，0），D（，0）, 设抛物线的解析式为y=ax2+k， 抛物线过点M和点B， 则k=5，a=﹣ , ∴抛物线解析式为：y=﹣x2+5； ∴当x=1时，y=； 当x=时，y= , ∴P（1， ），Q（， ）在抛物线上； 设竖直摆放圆柱形...
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：北师大版数学七年级下册第一章整式乘法1.2幂的乘方与积的乘方课时练习 题型：单选题

    （2x）3 等于（ ）

    A. －x7 B. x10 C. x9 D. 8x3

    D 【解析】试题解析： 故D项正确. 故选D.

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年八年级数学北师大版上册 第1-4章综合测试卷 题型：填空题

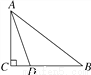
    如图，在Rt△ABC中，∠BCA＝90°，点D是BC上一点，AD＝BD，若AB＝8，BD＝5，则CD＝________．

    1.4 【解析】试题解析：设CD=x，则BC=5+x， 在Rt△ACD中, 在Rt△ABC中, 所以, 解得x=1.4， 即CD=1.4. 故答案为：1.4.

    查看答案和解析>>

    科目：初中数学 来源：北师大版九年级下册数学全册综合测试卷二 题型：解答题

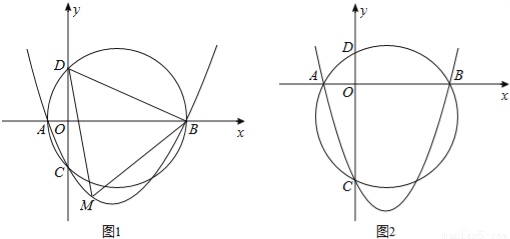
    如图，已知抛物线y=ax2+bx+c（a＞0，c＜0）交x轴于点A，B，交y轴于点C，设过点A，B，C三点的圆与y轴的另一个交点为D．

    （1）如图1，已知点A，B，C的坐标分别为（﹣2，0），（8，0），（0，﹣4）；

    ①求此抛物线的表达式与点D的坐标；

    ②若点M为抛物线上的一动点，且位于第四象限，求△BDM面积的最大值；

    （2）如图2，若a=1，求证：无论b，c取何值，点D均为定点，求出该定点坐标．

    （1）①，D（0，4）；②36；（2）证明见解析，（0，1）． 【解析】试题分析：（1）①利用待定系数法求抛物线的解析式；利用勾股定理的逆定理证明∠ACB=90°，由圆周角定理得AB为圆的直径，再由垂径定理知点C、D关于AB对称，由此得出点D的坐标. ②求出△BDM面积的表达式，再利用二次函数的性质求出最值. （2）根据抛物线与x轴的交点坐标、根与系数的关系、相似三角形求解． ...

    查看答案和解析>>

    科目：初中数学 来源：北师大版九年级下册数学全册综合测试卷二 题型：填空题

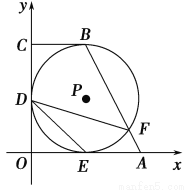
    如图，在直角坐标系中，四边形OABC是直角梯形，BC∥OA，⊙P分别与OA、OC、BC相切于点E、D、B，与AB交于点F.已知A(2，0)，B(1，2)，则tan∠FDE＝________．

    【解析】如图，连接PB、PE. ∵⊙P分别与OA、BC相切于点E、B， ∴PB⊥BC，PE⊥OA， ∵BC∥OA， ∴B、P、E在一条直线上， ∵A(2，0)，B(1，2)， ∴AE＝1，BE＝2， ∴tan∠ABE＝＝， ∵∠EDF＝∠ABE， ∴tan∠FDE＝.

    查看答案和解析>>

    科目：初中数学 来源：北师大版九年级下册数学全册综合测试卷二 题型：单选题

    一个圆锥的底面圆的周长是2π，母线长是3，则它的侧面展开图的圆心角等于（　　）

    A. 150°                                      B. 120°                                      C. 90°                                      D. 60°

    B 【解析】试题解析：设圆锥的侧面展开图的圆心角为n°， ∵圆锥的底面圆的周长是2π，母线长是3， ∴2π=， 解得n=120． 故选B．

    查看答案和解析>>

    科目：初中数学 来源：北师大版九年级下册数学全册综合测试卷二 题型：单选题

    把二次函数y=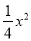+x﹣1化为y=a（x﹣h）2+k的形式是（　　）

    A. y=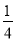（x+1）2+2 B. y=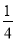（x+1）2﹣2 C. y=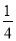（x﹣2）2+2 D. y=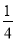（x+2）2﹣2

    D 【解析】试题解析：y=x2+x-1=（x2+4x+4）-1-1=（x+2）2-2． 故选D．

    查看答案和解析>>

    科目：初中数学 来源：北师大版九年级下册数学全册综合测试卷一 题型：解答题

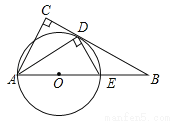
    如图，在△ABC中，∠C=90°，∠BAC的平分线交BC于点D，DE⊥AD，交AB于点E，AE为⊙O的直径．

    （1）判断BC与⊙O的位置关系，并证明你的结论；

    （2）求证：△ABD∽△DBE；

    （3）若cosB=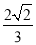，AE=4，求CD．

    （1）BC与⊙O相切；（2）证明见解析；（3）． 【解析】 试题分析：（1）结论：BC与⊙O相切，连接OD只要证明OD∥AC即可． （2）欲证明△ABD∽△DBE，只要证明∠BDE=∠DAB即可． （3）在Rt△ODB中，由cosB==，设BD=k，OB=3k，利用勾股定理列出方程求出k，再利用DO∥AC，得列出方程即可解决问题． 试题解析：（1）结论：BC与⊙O相切...

    查看答案和解析>>

    科目：初中数学 来源：人教版八年级下册数学全册综合测试二 题型：单选题

    能判定四边形ABCD为平行四边形的是（ ）．

    A. AB∥CD，AD=BC

    B. ∠A=∠B，∠C=∠D

    C. AB=CD，AD=BC

    D. AB=AD，CB=CD

    C 【解析】选项C中，两组对边分别相等的四边形是平行四边形．

    查看答案和解析>>

    同步练习册答案