
一个圆锥的底面圆的周长是2π,母线长是3,则它的侧面展开图的圆心角等于( )
A. 150° B. 120° C. 90° D. 60°
B 【解析】试题解析:设圆锥的侧面展开图的圆心角为n°, ∵圆锥的底面圆的周长是2π,母线长是3, ∴2π=, 解得n=120. 故选B.科目:初中数学 来源:北师大版数学七年级下册第一章整式乘法1.2幂的乘方与积的乘方课时练习 题型:单选题
-(a5)3 等于( )
A. -a15 B. a15 C. a8 D. -a9
A 【解析】试题解析:原式 故选A.查看答案和解析>>
科目:初中数学 来源:2017-2018学年八年级数学北师大版上册 第1-4章综合测试卷 题型:填空题
如图是某校的平面示意图的一部分,若用“(0,0)”表示图书馆的位置,“(0,-3)”表示校门的位置,则教学楼的位置可表示为
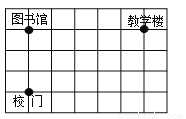
查看答案和解析>>
科目:初中数学 来源:北师大版九年级下册数学全册综合测试卷二 题型:填空题
如图,⊙O中OA⊥BC,∠CDA=25°,则∠AOB的度数为________.
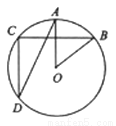
查看答案和解析>>
科目:初中数学 来源:北师大版九年级下册数学全册综合测试卷二 题型:填空题
如图,在水平地面点A处有一网球发射器向空中发射网球,网球飞行路线是一条抛物线,在地面上落点为B,有人在直线AB上点C(靠点B一侧)竖直向上摆放若干个无盖的圆柱形桶.试图让网球落入桶内,已知AB=4米,AC=3米,网球飞行最大高度OM=5米,圆柱形桶的直径为0.5米,高为0.3米(网球的体积和圆柱形桶的厚度忽略不计).当竖直摆放圆柱形桶至少________ 个时,网球可以落入桶内.
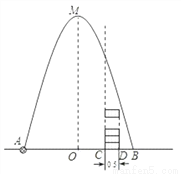
查看答案和解析>>
科目:初中数学 来源:北师大版九年级下册数学全册综合测试卷二 题型:单选题
若A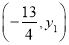 ,B
,B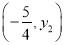 ,C
,C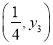 为二次函数y=x²+4x-5 的图象上的三点,则y1,y2,y3的大小关系是( )
为二次函数y=x²+4x-5 的图象上的三点,则y1,y2,y3的大小关系是( )
A. y1<y2<y3 B. y2<y1<y3 C. y3<y1<y2 D. y1<y3<y2
B 【解析】试题解析:∵y=x2+4x-5=(x+2)2-9, ∴对称轴是x=-2,开口向上, 距离对称轴越近,函数值越小, 比较可知,B(?,y2)离对称轴最近,C(,y3)离对称轴最远, 即y2<y1<y3. 故选B.查看答案和解析>>
科目:初中数学 来源:2017-2018学年度人教版九年级数学下册第26 章同步课时练习:26.1.1 反比例函数 题型:填空题
已知一个长方形的面积是20,那么这个长方形的长为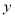 与宽为
与宽为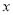 之间的函数关系式为___________.
之间的函数关系式为___________.
查看答案和解析>>
科目:初中数学 来源:北师大版九年级下册数学全册综合测试卷一 题型:填空题
某服装店购进单价为15元的童装若干件,销售一段时间后发现:当销售价为25元时平均每天能售出8件,而当销售价每降低1元,平均每天能多售出2件.当每件的定价为_______元时,该服装店平均每天的销售利润最大.
22 【解析】试题分析:设定价为x元时,利润为w元,由题意建立w与x的二次函数关系:w=(x-15)(×4+8),化简得:w=,∵-2<0,∴当x===22时,w有最大值,∴当每件的定价为22元时,该服装店平均每天的销售利润最大.查看答案和解析>>
科目:初中数学 来源:人教版八年级下册数学全册综合测试二 题型:单选题
已知反比例函数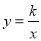 (x>0)的图象经过等腰三角形OAB(OB=AB)的顶点B,等腰三角形OAB的面积为2个平方单位,则k的值为( )
(x>0)的图象经过等腰三角形OAB(OB=AB)的顶点B,等腰三角形OAB的面积为2个平方单位,则k的值为( )
A. 1 B. 1.5 C. 2 D. 2.5
C 【解析】试题解析:作BC⊥x轴于C,如图, ∵三角形OAB为等腰三角形OAB, ∴OC=AC, ∴S△BOC=S△ABO=×2=1, ∴k=1, ∴k=2. 故选C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com