
���ڡ�C���C�ϵ�һ��A����ƽ���ڵĵ�P���㣺����AP���C���ڵ�Q����Q�������P�غϣ�����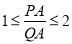 �����P��Ϊ��A���ڡ�C�ġ������㡱��
�����P��Ϊ��A���ڡ�C�ġ������㡱��
��֪��OΪ����ԭ�㣬��O�İ뾶Ϊ1����A��-1��0����
��1������P�ǵ�A���ڡ�O�ġ������㡱���ҵ�P��x���ϣ���д��һ�����������ĵ�P������________��
��2������B�ǵ�A���ڡ�O�ġ������㡱��������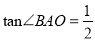 �����B��������t��ȡֵ��Χ��
�����B��������t��ȡֵ��Χ��
��3��ֱ��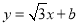 ��x�ύ�ڵ�M����y�ύ�ڵ�N�����߶�MN�ϴ��ڵ�A���ڡ�O�ġ������㡱��ֱ��д��b��ȡֵ��Χ��_____________________________��
��x�ύ�ڵ�M����y�ύ�ڵ�N�����߶�MN�ϴ��ڵ�A���ڡ�O�ġ������㡱��ֱ��д��b��ȡֵ��Χ��_____________________________��
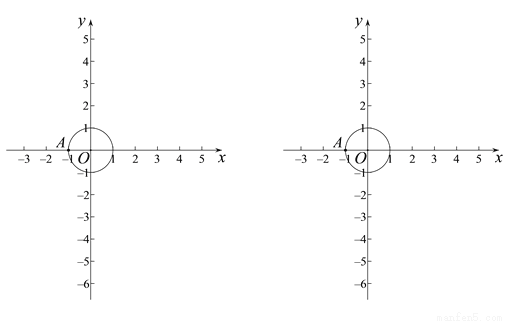

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ������ʡ2017-2018ѧ����꼶����Ԫ�µ�����ѧ�Ծ���2�� ���ͣ������
��һ���ĵ�(a��b)��(0����1)˳ʱ����ת180������õ������Ϊ____________��
����a����2��b�� ������������ת��ĵ�����Ϊ��x��y���� ��=0�� =-1�� ���x=-a��y=-2-b�� ���ԣ����õ������Ϊ��-a��-2-b���� �ʴ�Ϊ����-a��-2-b�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�����ɹ������첼��У2017-2018ѧ�����꼶��ѧ����ĩ������ѧ�Ծ� ���ͣ������
��ͼ����C���߶�AB��һ�㣬��M��N��P�ֱ����߶�AC��BC��AB���е㣬  ����
����
 �߶�AM�ij���
�߶�AM�ij���
 �߶�PN�ij���
�߶�PN�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�����ɹ������첼��У2017-2018ѧ�����꼶��ѧ����ĩ������ѧ�Ծ� ���ͣ���ѡ��
����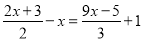 ȥ��ĸ�ã� ��
ȥ��ĸ�ã� ��
A. 3��2x+3��-x=2��9x-5��+6 B. 3��2x+3��-6x=2��9x-5��+1
C. 3��2x+3��-x=2��9x-5��+1 D. 3��2x+3��-6x=2��9x-5��+6
D �������������������������ͬ����6�ã�3(2x��3)��6x��2(9x��5)��6�� ��ѡD���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�����ɹ������첼��У2017-2018ѧ�����꼶��ѧ����ĩ������ѧ�Ծ� ���ͣ���ѡ��
��ɶ���ʽ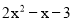 �ĵ���ʽ�����м����е�
�ĵ���ʽ�����м����е�
A. 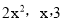 B.
B. 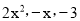 C.
C. 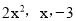 D.
D. 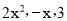
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�������к�����2018����꼶��ѧ����ĩ������ѧ�Ծ� ���ͣ������
�Ŵ���������ѧ��̩���ء������������Թ��ɶ����������ƹ��о�����ͼ��ͼ1��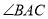 Ϊ��ǣ�ͼ2��
Ϊ��ǣ�ͼ2��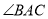 Ϊֱ�ǣ�ͼ3��
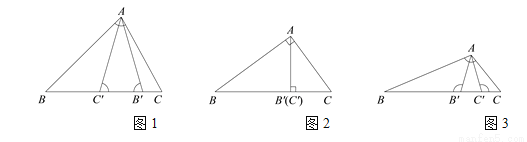
Ϊֱ�ǣ�ͼ3��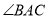 Ϊ�۽ǣ���
Ϊ�۽ǣ���
�ڡ�ABC�ı�BC��ȡ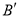 ��
�� 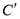 ���㣬ʹ
���㣬ʹ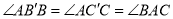 ����
����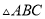 ��
��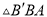 ��
��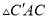 ��
�� 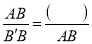 ��
�� 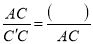 �������ɵ�
�������ɵ�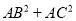
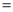 ������
������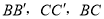 ��ʾ��
��ʾ��
��AB=4��AC=3��BC=6����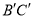
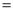 ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�������к�����2018����꼶��ѧ����ĩ������ѧ�Ծ� ���ͣ������
��ͬ������ʻ�Ļ���������Ӧ����ǰ���������Բ�ȡ�����ƶ���ʩ�İ�ȫ���룮��ͼ����һ��·�ڣ�һ����Ϊ10m�Ĵ�ͳ�����ƺ�ͣ�ھཻͨ�źŵ�20m��ֹͣ�ߴ���С�ż�ʻһ��С�γ������ͳ���ʻ����С�ž��ͳ�βx m������ͳ���������С�ŵ�ˮƽ����0.8m��������ظ���С�ŵ�ˮƽ����3.2m����С���ܿ���������ƣ���x����СֵΪ__________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2018��1�±����к�������������ѧ��ĩ�Ծ� ���ͣ������
��֪���κ���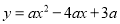 ��
��
��1���ö��κ���ͼ��ĶԳ�����x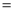 ��
��
��2�����ö��κ�����ͼ�����£���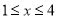 ʱ��
ʱ�� 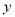 �����ֵ��2����
�����ֵ��2����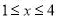 ʱ��
ʱ�� 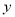 ����Сֵ��
����Сֵ��
��3�������ڸ��������ϵ�����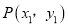 ��
�� 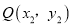 ����
����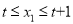 ��
�� 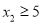 ʱ��������
ʱ��������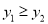 ������ͼ��ֱ��д��
������ͼ��ֱ��д��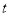 �����ֵ��
�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ2017-2018ѧ����꼶��ѧ�����п�����ѧ�Ծ� ���ͣ���ѡ��
��ͼ����ABC�У�AC=AD=BD����DAC=80º�����B�Ķ����ǣ� ��
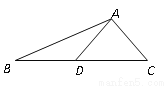
A. 40º B. 35º C. 25º D. 20º
C ������������������ڡ�ADC����AD=AC����DAC=80��á�ADC����������BD=AD�ɵá�B=��ADC=25�㣮 �������� ��AD=AC����DAC=80�㣬 ���ADC==50�㣬 �֡�AD=BD�� ���B=��BAD�� �ߡ�B+��BAD=��ADC�� ��2��B=��ADC�� ���B=��ADC=25�㣬 ��ѡ��C���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com