练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    已知直线DE与不等边△ABC的两边AC，AB分别交于点D，E，若∠CAB=60°，则图中∠CDE+∠BED=（　　）

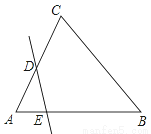
    A. 180°                                     B. 210°                                     C. 240°                                     D. 270°

    C 【解析】∵∠CAB=60°， ∴∠B+∠C=120°， 在四边形BCED中， ∠CDE+∠BED =360°-∠B-∠C=240°， 故选C.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：人教版八年级下册 第十六章 《二次根式》复习测试 题型：解答题

    由两个等腰直角三角形拼成的四边形（如图），已知AB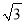＝，求：

    （1）四边形ABCD的周长；

    （2）四边形ABCD的面积．

    （1）4；（2）4.5. 【解析】试题分析：（1）由与是等腰直角三角形， 根据等腰直角三角形的性质求解即可求得与的长，继而求得答案； （2）由S四边形ABCD=S△ABD+S△CBD即可求得答案． 试题解析：(1)∵△ABD与△BCD是等腰直角三角形， ∴四边形ABCD的周长为： (2)S四边形ABCD=

    查看答案和解析>>

    科目：初中数学 来源：广东省汕头市龙湖区2017-2018学年八年级上学期期末质量检测数学试卷 题型：单选题

    花粉的质量很小，一粒某种植物花粉的质量约为0.000037毫克，那么0.000037毫克可用科学记数法表示为( )

    A. 0.37×10﹣5毫克 B. 3.7×10﹣6毫克 C. 37×10﹣7毫克 D. 3.7×10﹣5毫克

    D 【解析】绝对值小于1的负数也可以利用科学记数法表示，一般形式为a×10-n，与较大数的科学记数法不同的是其所使用的是负指数幂，指数由原数左边起第一个不为零的数字前面的0的个数所决定， 0.000037=3.7×10﹣5， 故选D.

    查看答案和解析>>

    科目：初中数学 来源：北师大版八年级下册数学 第一章 三角形的证明 单元检测卷 题型：填空题

    等腰三角形一腰上的高与另一腰的夹角为40°，则等腰三角形顶角的度数是 ________

    50或130 【解析】首先根据题意画出图形， 一种情况等腰三角形为锐角三角形，①如图1， ∵BD⊥AC，∠ABD=40°， ∴∠A=50°， 即顶角的度数为50°． 另一种情况等腰三角形为钝角三角形，②如图2， ∵BD⊥AC，∠DBA=40°， ∴∠BAD=50°， ∴∠BAC=130°． 故答案为：50或130．

    查看答案和解析>>

    科目：初中数学 来源：北师大版八年级下册数学 第一章 三角形的证明 单元检测卷 题型：单选题

    如下图，要用“HL”判断Rt△ABC和Rt△DEF全等的条件是（　　）

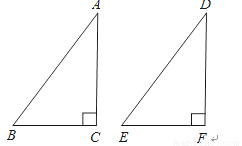
    A. AC=DF，BC=EF B. ∠A=∠D，AB=DE C. AC=DF，AB=DE D. ∠B=∠E，BC=EF

    C 【解析】∵在两个三角形中AB、DE是斜边， ∴只有C中，AC=DF、AB=DE符合， 故选C．

    查看答案和解析>>

    科目：初中数学 来源：人教版八年级下册数学 第19章 一次函数 单元检测卷 题型：解答题

    若一次函数y＝kx+4的图象经过点(1，2)．

    （1）求k的值；

    （2）在所给直角坐标系中画出此函数的图象．

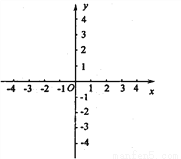
    （1）-2；（2）见解析 【解析】（1）把点（1，2）代入函数解析式，利用方程来求得k的值； （2）由两点确定一条直线进行作图． 【解析】 （1）依题意，得 2=k+4， 解得，k=-2，． 即k的值是-2； （2）由（1）得到该直线方程为y=-2x+4． 则当x=0时，y=4；当y=0时，x=2，即该直线经过点（0，4），（2，0），其图象如图所示： “点睛...

    查看答案和解析>>

    科目：初中数学 来源：人教版八年级下册数学 第19章 一次函数 单元检测卷 题型：填空题

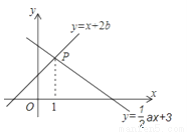
    如图，已知函数y=x+2b和y=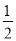ax+3的图象交于点P，则不等式x+2b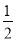＞ax+3的解集为________ ．

    x＞1 【解析】【解析】 由图象可知：当x＞1时， ．故答案为：x＞1．

    查看答案和解析>>

    科目：初中数学 来源：人教版七年级下册数学 第九章 不等式与不等式组 单元检测卷 题型：解答题

    园林部门用3600盆甲种花卉和2900盆乙种花卉搭配A、B两种园艺造型共50个，挂放在迎宾大道两侧，搭配每个造型所要花盆数如表，综合上述信息，解答下列问题．

    造型

    甲

    乙

    A

    90盆

    30盆

    B

    40盆

    100盆

    （1）符合题意的搭配方案有哪几种？

    （2）若搭配一个A种造型的成本为1000元，搭配一个B种造型的成本为1200元，选（1）中那种方案的成本最低？

    （1）见解析；（2）见解析 【解析】试题分析：（1）设需要搭配x个A种造型，则需要搭配B种造型（50-x）个，根据“用3600盆甲种花卉和2900盆乙种花卉搭配A、B两种园艺造型共50个”列不等式组求解，取整数值即可． （2）总成本为：1000x+1200（50-x）=60000-200x．利用一次函数的性质进行解答即可． 试题解析：【解析】 （1）设需要搭配x个A种造型，则需...

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级下册数学 第一章 整式的乘除 单元检测卷 题型：填空题

    （x﹣2y+1）（x﹣2y﹣1）=（________）2﹣（________）2=________．

    x﹣2y； 1； x2﹣4xy+4y2﹣1 【解析】（x﹣2y+1）（x﹣2y﹣1）=[（x-2y）+1][（x-2y）-1]=（x-2y）2﹣12= x2﹣4xy+4y2﹣1， 故答案为： x﹣2y； 1； x2﹣4xy+4y2﹣1 .

    查看答案和解析>>

    同步练习册答案