练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如下图，要用“HL”判断Rt△ABC和Rt△DEF全等的条件是（　　）

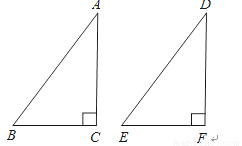
    A. AC=DF，BC=EF B. ∠A=∠D，AB=DE C. AC=DF，AB=DE D. ∠B=∠E，BC=EF

    C 【解析】∵在两个三角形中AB、DE是斜边， ∴只有C中，AC=DF、AB=DE符合， 故选C．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：人教版初中数学九年级上册第二十一章第一节《一元二次方程》提高练习 题型：单选题

    若px2－3x＋p2－p＝0是关于x的一元二次方程，则 （ ）

    A. p＝1 B. p＞0 C. p≠0 D. p为任意实数

    C 【解析】试题分析：∵方程px2－3x＋p2－p＝0是关于x的一元二次方程， ∴二次项系数P≠0． 故选C．

    查看答案和解析>>

    科目：初中数学 来源：广东省汕头市龙湖区2017-2018学年八年级上学期期末质量检测数学试卷 题型：填空题

    点(﹣3，﹣4)关于x轴对称点的坐标为______________．

    (-3，4) 【解析】关于x轴对称的点的坐标的特点是：横坐标不变，纵坐标互为相反数， 所以点(﹣3，﹣4)关于x轴对称点的坐标为(-3，4)， 故答案为：（-3，4）.

    查看答案和解析>>

    科目：初中数学 来源：北师大版八年级下册数学 第一章 三角形的证明 单元检测卷 题型：填空题

    如图所示，在四边形ABCD中，CB=CD，∠ABC=∠ADC=90°，∠BAC=35°，则∠BCD的度数为 ________度．

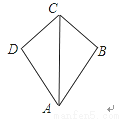
    110 【解析】∵∠ABC=∠ADC=90°，CB=CD，且CA=CA， ∴△ABC≌△ADC， ∴∠BCA=∠DCA， ∵∠BAC=35°，∠ABC=90°， ∴∠BCA=55°， ∴∠BCD=2∠BCA=110°， 故答案为：110．

    查看答案和解析>>

    科目：初中数学 来源：北师大版八年级下册数学 第一章 三角形的证明 单元检测卷 题型：填空题

    如图，在△ABC中，∠C=90°，BD平分∠ABC，若BD=5，BC=4，则点D到边AB的距离为________．

    3 【解析】∵在直角三角形ABC中，∠C=90°，BD=5，BC=4， ∴由勾股定理得CD为3，即为点D到BC的距离， ∵BD是∠ABC的平分线， 又∵角平线上点到角两边距离相等， ∴点D到AB距离等于点D到BC的距离， 即点D到AB的距离是3， 故答案为：3.

    查看答案和解析>>

    科目：初中数学 来源：北师大版八年级下册数学 第一章 三角形的证明 单元检测卷 题型：单选题

    已知直线DE与不等边△ABC的两边AC，AB分别交于点D，E，若∠CAB=60°，则图中∠CDE+∠BED=（　　）

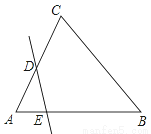
    A. 180°                                     B. 210°                                     C. 240°                                     D. 270°

    C 【解析】∵∠CAB=60°， ∴∠B+∠C=120°， 在四边形BCED中， ∠CDE+∠BED =360°-∠B-∠C=240°， 故选C.

    查看答案和解析>>

    科目：初中数学 来源：人教版八年级下册数学 第19章 一次函数 单元检测卷 题型：填空题

    如图，函数y=2x和y=ax+4的图象相交于点A（m，3），则不等式2x＞ax+4的解集为 ．

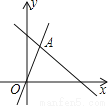
    【解析】 试题分析：首先利用待定系数法求出A点坐标，再以交点为分界，结合图象写出不等式2x＞ax+4的解集即可． 【解析】 ∵函数y=2x过点A（m，3）， ∴2m=3， 解得：m=， ∴A（，3）， ∴不等式2x＞ax+4的解集为x＞． 故答案为：

    查看答案和解析>>

    科目：初中数学 来源：人教版八年级下册数学 第19章 一次函数 单元检测卷 题型：单选题

    如图1，在矩形MNPQ中，动点R从点N出发，沿着N→P→Q→M方向运动至点M处停止，设点R运动的路程为x，△MNR的面积为y，如果y关于x的函数图象如图2所示，则下列说法不正确的是（　　）

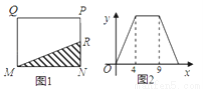
    A. 当x=2时，y=5         B. 矩形MNPQ的面积是20         C. 当x=6时，y=10         D. 当y=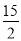时，x=10

    D 【解析】试题分析：由图2可知：PN=4，PQ=5． A、当x=2时，y=×MN×RN=×5×2=5，故A正确，与要求不符； B、矩形的面积=MN•PN=4×5=20，故B正确，与要求不符； C、当x=6时，点R在QP上，y=×MN×RN=10，故C正确，与要求不符； D、当y=时，x=3或x=10，故错误，与要求相符． 故选：D．

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级下册数学 第一章 整式的乘除 单元检测卷 题型：填空题

    如果3x﹣2的值为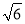， 那么9x2﹣12x+5的值是________．

    7 【解析】∵3x﹣2=， ∴9x2﹣12x+5=（9x2-12x+4）+1=（3x-2）2+1=+1=7， 故答案为：7.

    查看答案和解析>>

    同步练习册答案