
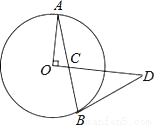
如图,AB是圆O的弦,OA⊥OD,AB,OD相交于点C,且CD=BD.
(1)判断BD与圆O的位置关系,并证明你的结论;
(2)当OA=3,OC=1时,求线段BD的长.
科目:初中数学 来源:2017年广东省佛山市中考数学模拟试卷(3) 题型:单选题
抛物线y=(x+2)2+1的顶点坐标是( )
A. (2,1) B. (2,﹣1) C. (﹣2,1) D. (﹣2,﹣1)
C 【解析】抛物线的顶点坐标为(-2,1). 故选C.查看答案和解析>>
科目:初中数学 来源:黑龙江省2017-2018学年八年级数学上学期期末试卷 题型:单选题
如图,从下列四个条件:①BC=B′C;②AC=A′C;③∠A′CA=∠B′CB;④AB=A′B′中,任取三个为条件,余下的一个为结论,则最多可以构成正确的结论的个数是( )
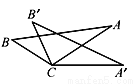
A. 1 B. 2
C. 3 D. 4
B 【解析】试题解析:当①②③为条件,④为结论时: ∵∠A′CA=∠B′CB, ∴∠A′CB′=∠ACB, ∵BC=B′C,AC=A′C, ∴△A′CB′≌△ACB, ∴AB=A′B′, 当①②④为条件,③为结论时: ∵BC=B′C,AC=A′C,AB=A′B′, ∴△A′CB′≌△ACB, ∴∠A′CB′=∠ACB, ∴∠A′CA=∠B′CB. 故选B.查看答案和解析>>
科目:初中数学 来源:2017-2018学年江苏省苏州市初三上期中模拟数学试卷 题型:单选题
抛物线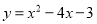 与
与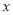 轴交于点
轴交于点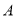 、
、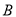 ,顶点为
,顶点为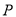 ,则
,则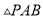 的面积是( ).
的面积是( ).
A. 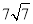 B.
B. 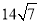 C.
C. 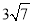 D.
D. 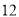
查看答案和解析>>
科目:初中数学 来源:2017-2018学年江苏省苏州市初三上期中模拟数学试卷 题型:单选题
如图,等腰三角形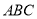 的顶角为
的顶角为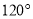 ,底边
,底边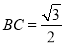 ,则腰长
,则腰长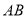 为( ).
为( ).

A. 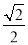 B.
B. 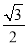 C.
C. 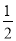 D.
D. 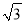
查看答案和解析>>
科目:初中数学 来源:2017年天津市中考数学模拟试卷 题型:填空题
若函数y﹦(m+1)x+m2﹣1是正比例函数,则m的值为_____.
1 【解析】∵y﹦(m+1)x+m2﹣1是正比例函数, ∴m+1≠0,m2﹣1=0, ∴m=1. 故答案为:1.查看答案和解析>>
科目:初中数学 来源:2017年天津市中考数学模拟试卷 题型:单选题
函数y= 中自变量x的取值范围是( )
中自变量x的取值范围是( )
A. x≤2 B. x≤2且x≠1 C. x<2且x≠1 D. x≠1
D 【解析】试题解析:根据二次根式有意义,分式有意义得:2-x≥0且x-1≠0, 解得:x≤2且x≠1. 故选B.查看答案和解析>>
科目:初中数学 来源:2017年四川省数学九年级(上)期末数学试卷 题型:填空题
若△ABC∽△A’B’C’,且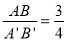 ,△ABC的周长为12cm,则△A’B’C’的周长为__________cm.
,△ABC的周长为12cm,则△A’B’C’的周长为__________cm.
查看答案和解析>>
科目:初中数学 来源:2017年安徽省中考数学模拟试卷 题型:解答题
如图①,在平面直角坐标系中,点A(0,3),点B(﹣3,0),点C(1,0),点D(0,1),连AB,AC,BD.
(1)求证:BD⊥AC;
(2)如图②,将△BOD绕着点O旋转,得到△B′OD′,当点D′落在AC上时,求AB′的长;
(3)试直接写出(Ⅱ)中点B′的坐标.
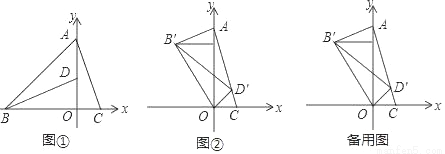
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com