练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    下列线段中，能成比例的是（　　）

    A. 3cm、6cm、8cm、9cm B. 3cm、5cm、6cm、9cm

    C. 3cm、6cm、7cm、9cm D. 3cm、6cm、9cm、18cm

    D 【解析】如果两条线段的乘积等于另外两条线段的乘积，则这四条线段叫作成比例线段.因此所给选项中，只有D符合，3×18=6×9，故选D.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：浙江省宁波市2017-2018学年八年级上册期末模拟数学试卷 题型：解答题

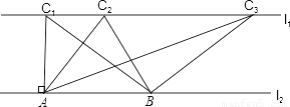
    如图，已知，l1∥l2 ， C1在l1上，并且C1A⊥l2 ，A为垂足，C2， C3是l1上任意两点，点B在l2上．设△ABC1的面积为S1， △ABC2的面积为S2， △ABC3的面积为S3， 小颖认为S1=S2=S3， 请帮小颖说明理由．

    S1=S2=S3 【解析】试题分析：根据两平行线间的距离相等和同底等高的两个三角形的面积相等即可解答． 试题解析：【解析】 ∵直线l1∥l2， ∴△ABC1，△ABC2，△ABC3的底边AB上的高相等， ∴△ABC1，△ABC2，△ABC3这3个三角形同底，等高， ∴△ABC1，△ABC2，△ABC3这些三角形的面积相等． 即S1=S2=S3．

    查看答案和解析>>

    科目：初中数学 来源：湖南省邵阳县黄亭市2017~2018学年九年级数学（上）期末综合检测模拟题 题型：单选题

    某地区家庭的年消费情况如下：年消费 10万元的有2 户，年消费 5万元的有1 户，年消费 1.5万元的有6户，年消费 7 千元的有1 户，可估计该地区每户年消费金额的一般水平为（ ）

    A. 1.5万元 B. 5万元 C. 10万元 D. 3.47万元

    D 【解析】试题解析：10户家庭的年消费的平均数为=3.47（万元）． 故该地每户年消费金额的一般水平为3.47万元． 故选D．

    查看答案和解析>>

    科目：初中数学 来源：2017年甘肃省兰州市中考数学模拟试卷 题型：填空题

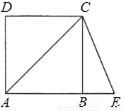
    如图，四边形ABCD是正方形，延长AB到E，使AE=AC，则∠BCE的度数是_____度．

    0.9m 【解析】试题分析：根据正方形的性质，易知∠CAE=∠ACB=45°；等腰△CAE中，根据三角形内角和定理可求得∠ACE的度数，进而可由∠BCE=∠ACE﹣∠ACB得出∠BCE的度数． 【解析】 ∵四边形ABCD是正方形， ∴∠CAB=∠BCA=45°； △ACE中，AC=AE，则： ∠ACE=∠AEC=（180°﹣∠CAE）=67.5°； ∴∠BCE...

    查看答案和解析>>

    科目：初中数学 来源：2017年甘肃省兰州市中考数学模拟试卷 题型：单选题

    某城市2014年底已有绿化面积300公顷，经过两年绿化，绿化面积逐年增加，到2016年底增加到363公顷，设绿化面积平均每年的增长率为x，由题意，所列方程正确的是( )

    A. 300(1＋x)=363 B. 300(1＋x)2=363 C. 300(1＋2x)=363 D. 363(1－x)2=300

    B 【解析】试题分析：知道2004年的绿化面积经过两年变化到2006，绿化面积成为363，设绿化面积平均每年的增长率为x，由题意可列出方程． 【解析】 设绿化面积平均每年的增长率为x， 300（1+x）2=363． 故选B．

    查看答案和解析>>

    科目：初中数学 来源：山东省诸城市2018届九年级上学期期中联考数学试卷（Word版）. 题型：解答题

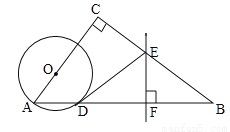
    如图，在△ABC中，∠C=90°，点O在AC上，以OA为半径的⊙O交AB于点D，BD的垂直平分线交BC于点E，交BD于点F，连接DE．

    （1）判断直线DE与⊙O的位置关系，并说明理由；

    （2）若AC=6，BC=8，OA=2，求线段DE的长．

    （1）直线DE与⊙O相切；（2）4.75． 【解析】试题分析：（1）连接OD，通过线段垂直平分线的性质和等腰三角形的性质证明∠EDB＋∠ODA＝90°，进而得出OD⊥DE，根据切线的判定即可得出结论； （2）连接OE，作OH⊥AD于H．则AH＝DH，由△AOH∽△ABC，可得，推出AH＝，AD＝，设DE＝BE＝x，CE＝8－x，根据OE2＝DE2＋OD2＝EC2＋OC2，列出方程即可解...

    查看答案和解析>>

    科目：初中数学 来源：山东省诸城市2018届九年级上学期期中联考数学试卷（Word版）. 题型：填空题

    若x1，x2是一元二次方程x2﹣2x﹣1=0的两个根，则x12﹣x1+x2的值为_____．

    3

    查看答案和解析>>

    科目：初中数学 来源：2017年河北省中考数学模拟试卷 题型：解答题

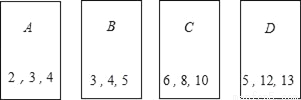
    在四张编号为A，B，C，D的卡片（除编号外，其余完全相同）的正面分别写上如图所示的正整数后，背面向上，洗匀放好．

    （1）我们知道，满足a2+b2=c2的三个正整数a，b，c成为勾股数，嘉嘉从中随机抽取一张，求抽到的卡片上的数是勾股数的概率P1；

    （2）琪琪从中随机抽取一张（不放回），再从剩下的卡片中随机抽取一张（卡片用A，B，C，D表示）．请用列表或画树形图的方法求抽到的两张卡片上的数都是勾股数的概率P2，并指出她与嘉嘉抽到勾股数的可能性一样吗？

    （1）；（2）淇淇与嘉嘉抽到勾股数的可能性不一样． 【解析】试题分析： （1）根据等可能事件的概率的定义，分别确定总的可能性和是勾股数的情况的个数； （2）用列表法列举出所有的情况和两张卡片上的数都是勾股数的情况即可. 试题解析： （1）嘉嘉随机抽取一张卡片共出现4种等可能结果，其中抽到的卡片上的数是勾股数的结果有3种，所以嘉嘉抽取一张卡片上的数是勾股数的概率P1=；...

    查看答案和解析>>

    科目：初中数学 来源：2017年辽宁省营口市大石桥市水源九年一贯制学校中考数学模拟试卷 题型：单选题

    如图，矩形ABCD中，AD=2AB，E、F、G、H分别是AB，BC，CD，AD边上的点，EG⊥FH，FH=2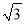，则四边形EFGH的面积为（　　）

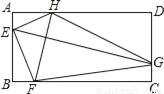
    A. 6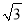 B. 12 C. 12 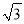D. 24

    B 【解析】过F作FM⊥AD于M，过E作EN⊥CD于N，根据矩形的性质和判定推出EN=2FH，求出EN的长，即可得出答案． 【解析】 过F作FM⊥AD于M，过E作EN⊥CD于N， 则∠FMH=∠ENG=90°， ∵四边形ABCD是矩形，EG⊥FH， ∴∠A=∠D=∠AEN=∠EOF=∠EZF=90°， ∴四边形AEND是矩形， ∴AD=EN， 同理AB=FM， ∵AD=...

    查看答案和解析>>

    同步练习册答案