练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，四边形ABCD是正方形，延长AB到E，使AE=AC，则∠BCE的度数是_____度．

    0.9m 【解析】试题分析：根据正方形的性质，易知∠CAE=∠ACB=45°；等腰△CAE中，根据三角形内角和定理可求得∠ACE的度数，进而可由∠BCE=∠ACE﹣∠ACB得出∠BCE的度数． 【解析】 ∵四边形ABCD是正方形， ∴∠CAB=∠BCA=45°； △ACE中，AC=AE，则： ∠ACE=∠AEC=（180°﹣∠CAE）=67.5°； ∴∠BCE...
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：浙江省宁波市2017-2018学年八年级上册期末模拟数学试卷 题型：单选题

    一个三角形的两边长分别为3 cm和7 cm，则此三角形的第三边的长可能是（ ）

    A. 3 cm B. 4 cm C. 7 cm D. 11 cm

    C 【解析】试题解析：设第三边长为xcm，根据三角形的三边关系可得： 7-3＜x＜7+3， 解得：4＜x＜10， 故答案为C．

    查看答案和解析>>

    科目：初中数学 来源：湖南省邵阳县黄亭市2017~2018学年九年级数学（上）期末综合检测模拟题 题型：填空题

    设反比例函数 y=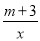，（x1，y1），（x2，y2）为其图象上两点，若x1＜0＜ x2，y1＞ y2，则m的取值范围是______．

    m＜-3 【解析】试题解析：∵x1＜0＜x2时，y1＞y2， ∴双曲线在第二，四象限， ∴m+3＜0， ∴m＜-3．

    查看答案和解析>>

    科目：初中数学 来源：2017年甘肃省兰州市中考数学模拟试卷 题型：解答题

    已知抛物线y=ax2+bx+c与x轴交于A、B两点，与y轴交于点C，其中点B在x轴的正半轴上，点C在y轴的正半轴上，线段OB、OC的长（OB＜OC）是方程x2﹣10x+16=0的两个根，且抛物线的对称轴是直线x=﹣2．

    （1）求A、B、C三点的坐标；

    （2）求此抛物线的表达式；

    （3）连接AC、BC，若点E是线段AB上的一个动点（与点A、点B不重合），过点E作EF∥AC交BC于点F，连接CE，设AE的长为m，△CEF的面积为S，求S与m之间的函数关系式，并写出自变量m的取值范围；

    （4）在（3）的基础上试说明S是否存在最大值？若存在，请求出S的最大值，并求出此时点E的坐标，判断此时△BCE的形状；若不存在，请说明理由．

    （1）A的坐标为（﹣6，0），点B的坐标为（2，0），点C的坐标为（0，8）；（2）y=﹣x2﹣x+8；（3）S=﹣m2+4m，自变量m的取值范围是0＜m＜8 ；（4）点E的坐标为（﹣2，0），△BCE为等腰三角形． 【解析】试题分析：（1）解方程x2﹣10x+16=0得x1=2，x2=8 ；根据点B、C的位置则可得B、C的坐标，再根据抛物线的对称性则可得点A的坐标； （2）根据（1）...

    查看答案和解析>>

    科目：初中数学 来源：2017年甘肃省兰州市中考数学模拟试卷 题型：解答题

    x2﹣4x+1=0（用配方法）

    x1=2+，x2=2﹣. 【解析】试题分析：先移项，然后配方，解出x即可. 试题解析：x2－4x+1=0， 移项，得x2－4x=－1， 配方，得x2－4x+4=－1+4，即（x－2）2=3， 解得，x－2=， 即x1=2+，x2=2－.

    查看答案和解析>>

    科目：初中数学 来源：2017年甘肃省兰州市中考数学模拟试卷 题型：单选题

    正多边形的中心角与该正多边形一个内角的关系是（　　）

    A. 互余 B. 互补 C. 互余或互补 D. 不能确定

    B 【解析】设正多边形的边数为n，则正多边形的中心角为，正多边形的一个外角等于，所以正多边形的中心角等于正多边形的一个外角，而正多边形的一个外角与该正多边形相邻的一个内角的互补，所以正多边形的中心角与该正多边形一个内角互补． 故选B．

    查看答案和解析>>

    科目：初中数学 来源：2017年甘肃省兰州市中考数学模拟试卷 题型：单选题

    下列线段中，能成比例的是（　　）

    A. 3cm、6cm、8cm、9cm B. 3cm、5cm、6cm、9cm

    C. 3cm、6cm、7cm、9cm D. 3cm、6cm、9cm、18cm

    D 【解析】如果两条线段的乘积等于另外两条线段的乘积，则这四条线段叫作成比例线段.因此所给选项中，只有D符合，3×18=6×9，故选D.

    查看答案和解析>>

    科目：初中数学 来源：山东省诸城市2018届九年级上学期期中联考数学试卷（Word版）. 题型：单选题

    如图，AB是半圆半径，半径OC⊥AB于点O，点D是弧BC的中点，连接CD、AD、OD，给出以下四个结论：①∠DOB=∠ADC；②CE=OE；③△ODE∽△ADO；④2CD2=CE·AB．其中正确结论的序号是（　　）

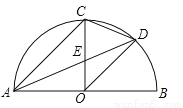
    A. ①③ B. ②④ C. ①④ D. ①②③

    C 【解析】试题分析：①∵AB是半圆直径，∴AO=OD，∴∠OAD=∠ADO，∵AD平分∠CAB交弧BC于点D， ∴∠CAD=∠DAO=∠CAB， ∴∠CAD=∠ADO， ∴AC∥OD， ∴∠DOB=∠CAO，又∵∠CAO=∠ADC（都对着半圆弧），∴∠DOB=∠ADC故①正确； ②由题意得，OD=R，AC=R， ∵OE：CE=OD：AC=1： ， ∴OE≠CE，故②错误；...

    查看答案和解析>>

    科目：初中数学 来源：2017年辽宁省营口市大石桥市水源九年一贯制学校中考数学模拟试卷 题型：解答题

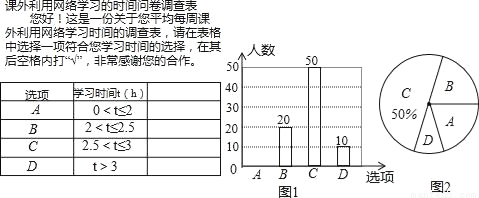
    随着教育信息化的发展，学生的学习方式日益增多，教师为了指导学生有效利用网络进行学习，对学生进行了随机问卷调查（问卷调查表如图所示），并用调查结果绘制了图1、图2两幅统计图（均不完整），请根据统计图解答以下问题：

    （1）本次接受问卷调查的学生共有　 　人，在扇形统计图中“D“选项所占的百分比为　 　；

    （2）扇形统计图中，“B”选项所对应扇形圆心角为　 　度；

    （3）请补全条形统计图；

    （4）若该校共有1200名学生，请您估计该校学生课外利用网络学习的时间在“A”选项的有多少人？

    （1）100，10%；（2）72；（3）补图见解析；（4）240人. 【解析】由条形统计图与扇形统计图获得的数据： 因为图（1）、图（2）中已知C选项的百分比与人数，由C选项的百分比=×100％求解； 先求出B选项的百分比，再利用扇形统计图的圆心角的度数=360°×B选项的百分比求解； （3）由（1）所得总人数求出B选项的人数即可作图； （4）先求出A选项的百分比即可...

    查看答案和解析>>

    同步练习册答案