
计算:
(1)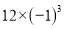 -
-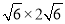 ÷
÷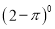 ;
;
(2)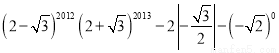
科目:初中数学 来源:人教版九年级上册数学 23.2.3关于原点对称的点的坐标 练习 题型:解答题
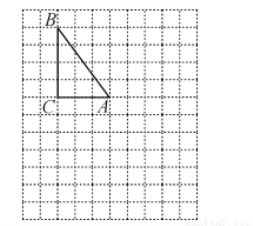
在下列的网格图中.每个小正方形的边长均为1个单位,在Rt△ABC中,∠C=90°,AC=3,BC=4.
(1)试在图中作出△ABC以A为旋转中心,沿顺时针方向旋转90°后的图形△AB1C1;
(2)若点B的坐标为(-3,5),试在图中画出直角坐标系,并标出A、C两点的坐标;
(3)根据(2)中的坐标系作出与△ABC关于原点对称的图形△A2B2C2,并标出B2、C2两点的坐标.
查看答案和解析>>
科目:初中数学 来源:2017年秋人教版数学九年级上册 第23章 旋转 全章测试卷 题型:解答题
如图,把△AOB绕点O逆时针旋转40°可得到△A′OB′.
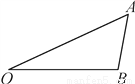
(1)画出旋转后的图形;
(2)指出旋转角的度数并找出一组对应边.
(1)图形见解析; (2)旋转角∠AOA′=∠BOB′=40°,OA,OA′或OB,OB′或AB,A′B′是一组对应边. 【解析】试题分析:(1)作出△AOB绕点O逆时针旋转40°后的图形△A′OB′即可; (2)根据A和A′,B和B′O和O是对应点,得出旋转角和对应边即可. 试题解析:【解析】 (1)作图如下: (2)旋转角∠AOA′=∠BOB′=40°,OA,O...查看答案和解析>>
科目:初中数学 来源:2017年秋人教版数学九年级上册 第23章 旋转 全章测试卷 题型:单选题
如图,P是等腰直角△ABC外一点,把BP绕点B顺时针旋转90°到BP′,已知∠AP′B=135°,P′A∶P′C=1∶3,则P′A∶PB=( )
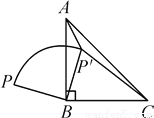
A. 1∶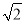 B. 1∶2 C.
B. 1∶2 C. 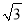 ∶2 D. 1∶
∶2 D. 1∶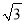
查看答案和解析>>
科目:初中数学 来源:广东省深圳外国语学校2017-2018学年八年级上学期期中考试数学试卷 题型:解答题
在平面直角坐标系中.
(1)已知点P(2a-6,a+4)在y轴上,求点P的坐标;
(2)已知两点A(-3,m-1),B(n+1,4)若AB∥x 轴,点B在第一象限,求m的值,并确定n的取值范围;
(3)在(1)(2)的条件下,如果线段 AB 的长度是6,试判断以P、A、B为顶点的三角形的形状,并说明理由.
(1) (0,7);(2) m=5,n>﹣1;(3) △PAB 是等腰直角三角形,理由见解析. 【解析】试题分析: (1)由y轴上的点的横坐标为0,得2a-6=0,即可; (2)由平行x轴的直线上的点的纵坐标相等列方程,注意点B的位置; (3)由(1)(2)得P(0,7),A(-3,4),(3,4),用勾股定理计算PA,PB,AB的长即可. 【解析】 (1)根据题意...查看答案和解析>>
科目:初中数学 来源:广东省深圳外国语学校2017-2018学年八年级上学期期中考试数学试卷 题型:单选题
关于x,y的方程组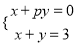 的解是
的解是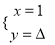 ,其中y的值被盖住了,不过仍能求出p,则p的值是( )
,其中y的值被盖住了,不过仍能求出p,则p的值是( )
A. ﹣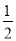 B.
B. 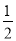 C. ﹣
C. ﹣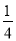 D.
D. 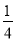
查看答案和解析>>
科目:初中数学 来源:广东省深圳外国语学校2017-2018学年八年级上学期期中考试数学试卷 题型:单选题
下列函数中,是一次函数的有( )
(1)y=πx;(2)y=2x﹣1;(3)y= ;(4)y=2﹣3x;(5)y=x2﹣1.
;(4)y=2﹣3x;(5)y=x2﹣1.
A. 4个 B. 3个 C. 2个 D. 1个
C 【解析】y=πx属于正比例函数,是特殊的一次函数,属于一次函数;y=2x?1,y=2?3x符合一次函数的定义,属于一次函数,y=属于反比例函数,y=x2﹣1属于二次函数.综上所述,一次函数的个数是3个。故选:B.查看答案和解析>>
科目:初中数学 来源:人教版九年级上册数学 23.1图形的旋转(1)测试 题型:填空题
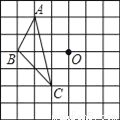
如图,在方格纸中,每个小方格都是边长为1cm的正方形,△ABC的三个顶点都在格点上,将△ABC绕点O逆时针旋转90°后得到△A′B′C′(其中A、B、C的对应点分别为A′,B′,C′,则点B在旋转过程中所经过的路线的长是______cm.(结果保留π)
查看答案和解析>>
科目:初中数学 来源:贵州省六盘水市2018届九年级上学期第二次月考数学试卷 题型:单选题
如图,A,B两地被池塘隔开,小明通过下列方法测出了A,B间的距离:先在AB外选一点C,然后测出AC,BC的中点M,N,并测量出MN的长为12 m,由此他就知道了A,B间的距离,有关他这次探究活动的描述错误的是( )
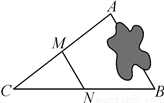
A. AB=24 m B. MN∥AB C. △CMN∽△CAB D. CM∶MA=1∶2
【答案】D
【解析】试题分析:根据三角形的中位线平行于第三边并且等于第三边的一半可得MN∥AB,MN=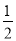 AB,再根据相似三角形的判定解答.
AB,再根据相似三角形的判定解答.
试题解析:∵M、N分别是AC,BC的中点
∴MN∥AB,MN=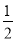 AB,
AB,
∴AB=2MN=2×12=24m
△CMN∽△CAB
∵M是AC的中点
∴CM=MA
∴CM:MA=1:1
故描述错误的是D选项.
故选D.
考点:1.三角形中位线定理;2.相似三角形的应用.
【题型】单选题
【结束】
10
若关于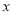 的一元二次方程
的一元二次方程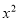 +x-3m=0有两个不相等的实数根,则
+x-3m=0有两个不相等的实数根,则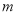 的取值范围是( )
的取值范围是( )
A. 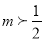 B.
B. 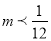 C.
C. 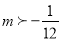 D.
D. 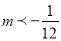
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com