
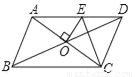
如图,?ABCD的周长为20cm,AC与BD相交于点O,OE⊥AC交AD于E,则△CDE的周长为( )
A. 6cm B. 8cm C. 10cm D. 12cm
C 【解析】试题分析:本题考查了平行四边形的性质、线段垂直平分线的性质以及三角形周长的计算;熟练掌握平行四边形的性质,运用线段垂直平分线的性质得出AE=CE是解决问题的关键。∵四边形ABCD是平行四边形,∴AB=DC,AD=BC,OA=OC, ∵?ABCD的周长为20cm, ∴AD+DC=10cm, 又∵OE⊥AC, ∴AE=CE, ∴△CDE的周长=DE+CE+DC=DE+AE+DC... 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:初中数学 来源:江苏省2018届九年级上学期期末模拟数学试卷 题型:单选题
已知点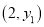 ,
, 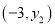 均在抛物线
均在抛物线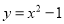 上,则
上,则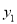 、
、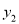 的大小关系为( )
的大小关系为( )
A. 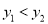 B.
B. 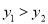 C.
C. 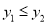 D.
D. 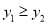
查看答案和解析>>
科目:初中数学 来源:2017年湖南省郴州市中考数学模拟试卷 题型:填空题
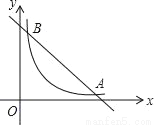
如图,在直角坐标系中,直线y=6﹣x与双曲线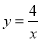 (x>0)的图象相交于A、B,设点A的坐标为(m,n),那么以m为长,n为宽的矩形的面积和周长分别为_____,_____.
(x>0)的图象相交于A、B,设点A的坐标为(m,n),那么以m为长,n为宽的矩形的面积和周长分别为_____,_____.
查看答案和解析>>
科目:初中数学 来源:2017年湖北省中考数学模拟试卷 题型:解答题
某文具店销售甲、乙两种圆规,当销售5只甲种、1只乙种圆规,可获利润25元,销售6只甲种、3只乙种圆规,可获利润39元.
(1)问该文具店销售甲、乙两种圆规,每只的利润分别是多少元?
(2)在(1)中,文具店共销售甲、乙两种圆规50只,其中甲种圆规为a只,求文具店所获得利润P与a的函数关系式,并求当a≥30时P的最大值.
(1)甲种圆规每只的利润是4元,乙种圆规每只的利润是5元;(2)220. 【解析】试题分析:(1)设文具店销售甲、乙两种圆规,每只的利润分别是x元、y元,根据题意“销售5只甲种、1只乙种圆规,可获利润25元,销售6只甲种、3只乙种圆规,可获利润39元”,列出的方程组,解方程组即可;(2)根据题意可以列出文具店所获利p与a的函数关系式,然后根据当a≥30,可以求得p的最大值即可. 试题解...查看答案和解析>>
科目:初中数学 来源:2017年湖北省中考数学模拟试卷 题型:填空题
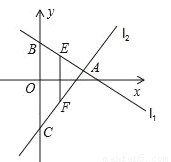
如图,已知直线l1:y=k1x+4与直线l2:y=k2x﹣5交于点A,它们与y轴的交点分别为点B,C,点E,F分别为线段AB、AC的中点,则线段EF的长度为______.
查看答案和解析>>
科目:初中数学 来源:2017年湖北省中考数学模拟试卷 题型:单选题
下列说法中正确的是( )
A. “打开电视机,正在播放《动物世界》”是必然事件
B. 某种彩票的中奖率为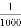 ,说明每买1 000张彩票,一定有一张中奖
,说明每买1 000张彩票,一定有一张中奖
C. 抛掷一枚质地均匀的硬币一次,出现正面朝上的概率为
D. 想了解长沙市所有城镇居民的人均年收入水平,宜采用抽样调查
D 【解析】试题分析:根据随机事件,可判断A;根据概率的意义,可判断B、C;根据调查方式,可判断D. 【解析】 A、“打开电视机,正在播放《动物世界》”是随机事件,故A错误; B、某种彩票的中奖概率为,说明每买1000张,有可能中奖,也有可能不中奖,故B错误; C、抛掷一枚质地均匀的硬币一次,出现正面朝上的概率为,故C错误; D、想了解长沙市所有城镇居民的人均年收入...查看答案和解析>>
科目:初中数学 来源:山东省2017-2018学年八年级上期末模拟数学试卷 题型:解答题
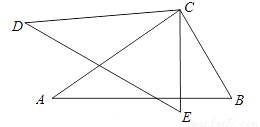
如图,CE=CB,CD=CA,∠DCA=∠ECB,求证:DE=AB.
查看答案和解析>>
科目:初中数学 来源:山东省2017-2018学年八年级上期末模拟数学试卷 题型:单选题
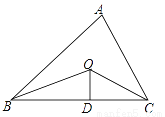
如图,已知△ABC的周长是21,OB,OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=4,△ABC的面积是( )
A. 25 B. 84 C. 42 D. 21
C 【解析】连接OA,作OE⊥AB于E,OF⊥AC于F, 又∵OB,OC分别平分∠ABC和∠ACB,OD⊥BC, ∴OD=OE=4,OD=OF=4, ∴S△ABC=S△AOB+S△BOC+S△AOC=•OE•AB+ •OD•BC+ •OF•AC= ×4×(AB+BC+AC)= ×4×21=42, 故选C.查看答案和解析>>
科目:初中数学 来源:安徽省2018届九年级上学期第二次月考数学试卷 题型:单选题
已知二次函数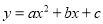 的图象如图所示,有以下结论:①
的图象如图所示,有以下结论:①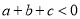 ;②
;②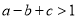 ;③
;③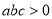 ;④
;④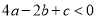 ;⑤
;⑤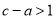 其中所有正确结论的序号是( )
其中所有正确结论的序号是( )
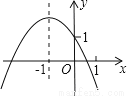
A. ①② B. ①③④ C. ①②③⑤ D. ①②③④⑤
C 【解析】试题解析:①当x=1时,y=a+b+c<0,故①正确, ②当x=-1时,y=a-b+c>2,故②正确, ③由抛物线的开口向下知a<0,与y轴的交点为在y轴的正半轴上, ∴c>0,对称轴为x=-=-1,得2a=b, ∴a、b同号,即b<0, ∴abc>0,故③正确, ④∵对称轴为x=-=-1, ∴点(0,2)的对称点为(-2,2), ...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com