
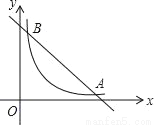
如图,在直角坐标系中,直线y=6﹣x与双曲线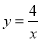 (x>0)的图象相交于A、B,设点A的坐标为(m,n),那么以m为长,n为宽的矩形的面积和周长分别为_____,_____.
(x>0)的图象相交于A、B,设点A的坐标为(m,n),那么以m为长,n为宽的矩形的面积和周长分别为_____,_____.
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:初中数学 来源:2017-2018学年江苏苏州姑苏区第十中学初二上期中试卷数学试卷 题型:单选题
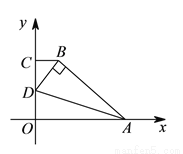
如图,在平面直角坐标系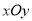 中,已知
中,已知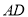 平分
平分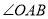 ,
, 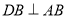 ,
, 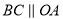 ,点
,点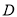 的坐标为
的坐标为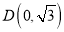 ,点
,点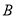 的横坐标为
的横坐标为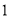 ,则点
,则点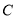 的坐标是( ).
的坐标是( ).
A. 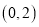 B.
B. 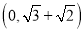 C.
C. 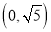 D.
D. 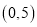
查看答案和解析>>
科目:初中数学 来源:山东省临朐县沂山风景区2017-2018学年七年级上期末模拟数学试卷 题型:解答题
在数轴上表示下列各数,并用“>”把它们连起来:﹣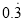 ,﹣
,﹣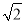 ,0,
,0, 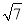 ,
, 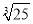 ,π,﹣3.14.
,π,﹣3.14.
查看答案和解析>>
科目:初中数学 来源:山东省临朐县沂山风景区2017-2018学年七年级上期末模拟数学试卷 题型:单选题
下列几何体中,属于棱柱的是( )
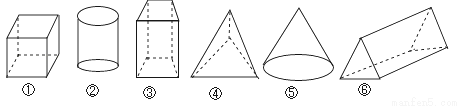
A. ①③ B. ① C. ①③⑥ D. ①⑥
C 【解析】所给几何体依次为:①棱柱;②圆柱;③棱柱;④棱锥;⑤圆锥;⑥棱柱,属于棱柱的有①③⑥, 故选C.查看答案和解析>>
科目:初中数学 来源:2017年湖南省郴州市中考数学模拟试卷 题型:解答题
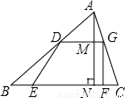
如图,已知△ABC中,AB>AC,BC=6,BC边上的高AN=4.直角梯形DEFG的底EF在BC边上,EF=4,点D、G分别在边AB、AC上,且DG∥EF,GF⊥EF,垂足为F.设GF的长为x,直角梯形DEFG的面积为y,求y关于x的函数关系式,并写出函数的定义域.
查看答案和解析>>
科目:初中数学 来源:2017年湖南省郴州市中考数学模拟试卷 题型:单选题
已知抛物线和直线l在同一直角坐标系中的图象如图所示,抛物线的对称轴为直线x=﹣1,P1(x1,y1),P2(x2,y2)是抛物线上的点,P3(x3,y3)是直线l上的点,且x3<﹣1<x1<x2,则y1,y2,y3的大小关系是( )
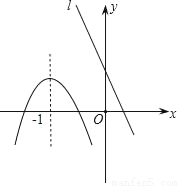
A. y1<y2<y3 B. y2<y3<y1 C. y3<y1<y2 D. y2<y1<y3
D 【解析】因为抛物线的对称轴为直线x=-1,开口向下,P1(x1,y1),P2(x2,y2)是抛物线上的点,且-1<x1<x2,根据二次函数的性质:在对称轴的右侧,y随x的增大而减小,可得y2< y1;P3(x3,y3)是直线l上的点,直线y随x的增大而减小,且x3<-1,由图象可知,直线上x3对应的函数值y3大于-1对应的函数值,又因x=-1时,抛物线的顶点最高,可得y3最大,所以y2<...查看答案和解析>>
科目:初中数学 来源:2017年湖南省郴州市中考数学模拟试卷 题型:单选题
下列运算正确的是( )
A. 3a2+5a2=8a4 B. a6•a2=a12 C. (a+b)2=a2+b2 D. (a2+1)0=1
D 【解析】试题分析:A、原式合并同类项得到结果,即可做出判断; B、原式利用同底数幂的乘法法则计算得到结果,即可做出判断; C、原式利用完全平方公式展开得到结果,即可做出判断; D、原式利用零指数幂法则计算得到结果,即可做出判断. 【解析】 A、原式=8a2,故A选项错误; B、原式=a8,故B选项错误; C、原式=a2+b2+2ab,故C选项错误; ...查看答案和解析>>
科目:初中数学 来源:2017年湖北省中考数学模拟试卷 题型:单选题
如图,?ABCD的周长为20cm,AC与BD相交于点O,OE⊥AC交AD于E,则△CDE的周长为( )
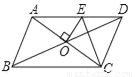
A. 6cm B. 8cm C. 10cm D. 12cm
C 【解析】试题分析:本题考查了平行四边形的性质、线段垂直平分线的性质以及三角形周长的计算;熟练掌握平行四边形的性质,运用线段垂直平分线的性质得出AE=CE是解决问题的关键。∵四边形ABCD是平行四边形,∴AB=DC,AD=BC,OA=OC, ∵?ABCD的周长为20cm, ∴AD+DC=10cm, 又∵OE⊥AC, ∴AE=CE, ∴△CDE的周长=DE+CE+DC=DE+AE+DC...查看答案和解析>>
科目:初中数学 来源:吉林省长春汽车经济技术开发区2017-2018学年八年级上学期期末教学质量跟踪测试数学试卷 题型:解答题
如图,在4×4的正方形网格中,每个小正方形的边长均为1.请在所给网格中画一个边长分别为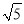 、2
、2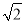 、3的三角形.
、3的三角形.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com