
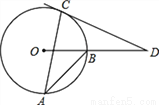
如图,AB、AC是⊙O的两条弦∠A=25°,过点C的切线与OB的延长线交于点D,则∠D的度数是_________.
科目:初中数学 来源:江苏省连云港市灌云县2017-2018学年七年级(上)期中数学试卷 题型:单选题
把(+5)﹣(+3)﹣(﹣1)+(﹣5)写成省略括号的和的形式是( )
A. ﹣5﹣3+1﹣5 B. 5﹣3﹣1﹣5 C. 5+3+1﹣5 D. 5﹣3+1﹣5
D 【解析】试题解析:原式=(+5)+(﹣3)+(+1)+(﹣5)=5﹣3+1﹣5. 故选D.查看答案和解析>>
科目:初中数学 来源:福建省上杭县城区片2017-2018学年第一学期三校联考及答案 题型:解答题
计算:
(1)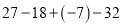 ; (2)
; (2)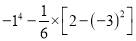 .
.
查看答案和解析>>
科目:初中数学 来源:福建省上杭县城区片2017-2018学年第一学期三校联考及答案 题型:单选题
绝对值等于7的数是( ).
A. 7 B. 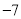 C.
C. 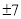 D. 0和7
D. 0和7
查看答案和解析>>
科目:初中数学 来源:安徽省合肥市2016-2017学年度第一学期期末教学质量检测 九年级数学试卷 题型:解答题
反比例函数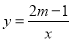 的图象如图所示,A(-1,b1),B(-2,b2)是该图象上的两点.
的图象如图所示,A(-1,b1),B(-2,b2)是该图象上的两点.
(1)比较b1与b2的大小;
(2)求m的取值范围.

查看答案和解析>>
科目:初中数学 来源:安徽省合肥市2016-2017学年度第一学期期末教学质量检测 九年级数学试卷 题型:单选题
在学校组织的实践活动中,小新同学用纸板制作了一个圆锥模型,它的底面半径为1,高为2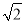 ,则这个圆锥的侧面积是( )
,则这个圆锥的侧面积是( )
A. 3π B. 4π C. 2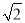 π D. 2π
π D. 2π
查看答案和解析>>
科目:初中数学 来源:2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷(七) 题型:解答题
如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B两点,A点在原点的左侧,B点的坐标为(3,0),与y轴交于C(0,﹣3)点,点P是直线BC下方的抛物线上一动点.
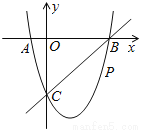
(1)求这个二次函数的表达式.
(2)连接PO、PC,并把△POC沿CO翻折,得到四边形POP′C,那么是否存在点P,使四边形POP′C为菱形?若存在,请求出此时点P的坐标;若不存在,请说明理由.
(3)当点P运动到什么位置时,四边形ABPC的面积最大?求出此时P点的坐标和四边形ABPC的最大面积.
(1)y=x2-2x-3;(2)点P(,-);(3)当x=时,四边形ABPC的面积最大.此时P点的坐标为(,-),四边形ABPC的面积. 【解析】试题分析:(1)将B、C的坐标代入抛物线的解析式中即可求得待定系数的值; (2)由于菱形的对角线互相垂直平分,若四边形POP′C为菱形,那么P点必在OC的垂直平分线上,据此可求出P点的纵坐标,代入抛物线的解析式中即可求出P点的坐标; (...查看答案和解析>>
科目:初中数学 来源:2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷(七) 题型:单选题
口袋中放有3只红球和11只黄球,这两种球除颜色外没有任何区别,随机从口袋中任取一只球,取得黄球的可能性的大小是( )
A. 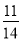 B.
B. 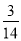 C.
C. 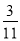 D.
D. 
查看答案和解析>>
科目:初中数学 来源:山东省2017-2018学年八年级12月月考数学试卷 题型:解答题
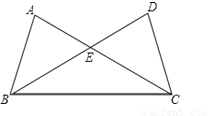
如图,△ABC与△DCB中,AC与BD交于点E,且∠A=∠D,AB=DC.
(1)求证:△ABE≌△DCE;
(2)当∠AEB=50°,求∠EBC的度数?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com