练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

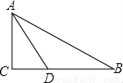
    如图，在Rt△ABC中，∠C=90°，AD平分∠BAC交BC于点D，若∠B=30°，BD=6，则CD的长为_____．

    3 【解析】∵在Rt△ABC中,∠C=90°,∠B=30°， ∴∠BAC=60°. 又AD平分∠BAC， ∴∠BAD=∠CAD=30°， ∴∠BAD=∠B=30°， ∴AD=BD=6， ∴CD=AD=3. 故答案为：3.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2017年天津二十一中中考数学冲刺试卷（2） 题型：单选题

    反比例函数y=﹣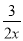中常数k为（　　）

    A. ﹣3 B. 2 C. ﹣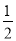 D. ﹣

    D 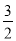【解析】根据题意，由反比例函数y=﹣中常数k为﹣， 故选：D．

    查看答案和解析>>

    科目：初中数学 来源：2017年贵州省中考数学二模试卷 题型：解答题

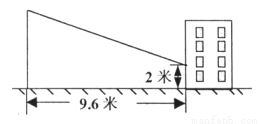
    小亮同学想利用影长测量学校旗杆的高度，如图，他在某一时刻测得1米长的竹杆其影长为1.2米，同时旗杆的影子一部分在地面上，另一部分在某一建筑的墙上，分别测得其长度为9.6米和2米，则学校旗杆的高度为______米。

    10 【解析】 试题分析：根据相似的性质可得：1:1.2=x：9.6，则x=8，则旗杆的高度为8+2=10米.

    查看答案和解析>>

    科目：初中数学 来源：2017年吉林省长春市中考数学模拟试卷（7） 题型：解答题

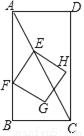
    如图，在矩形ABCD中，AB=4，BC=2，点E从点A出发，以每秒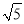个单位长度的速度沿对角线AC向终点C运动，点F从点B出发，以每秒2个单位长度的速度沿边BA向终点A运动，连结EF，将线段EF绕点F顺时针旋转90°得到线段FG，以EF，FG为边作正方形EFGH，设点E运动的时间为t秒（t＞0）．

    （1）用含t的代数式表示点E到边AB的距离．

    （2）当点G落在边AB上时，求t的值．

    （3）连结BG，设△BFG的面积为S平方单位（S＞0），求S与t之间的函数关系式．

    （4）直接写出当正方形EFGH的顶点与点B，D距离相等时的t值．

    （1）点E到边AB的距离为t（2）t=1（3）S= （4）当正方形EFGH的顶点与点B，D距离相等时的t值为s或1s或s 【解析】试题分析：（1）如图1中，作EM⊥AB于M．由EM∥BC，可得，即，延长即可解决问题； （2）如图2中，G在AB边时，由AF+FB=4，可得2t+2t=4，解方程即可； （3）分两种情形①如图3中，当0

    查看答案和解析>>

    科目：初中数学 来源：2017年吉林省长春市中考数学模拟试卷（7） 题型：解答题

    我校为了创建书香校园，去年购进一批图书，经了解，科普书的单价比文学书的单价多4元，用12000元购进的科普书与用8000元购进的文学书本数相等．求文学和科普书的单价．

    文学书的单价为8元，科普书的单价为12元． 【解析】试题分析：首先设文学书的单价为x元，则科普书的单价为（x+4）元，根据题意可得等量关系：12000元购进的科普书是数量=用8000元购进的文学书本数，根据等量关系列出方程，再解即可． 试题解析：设文学书的单价为x元。 根据题意，得 解得x=8. 经检验，x=8是原方程的解，且符合题意， 8+4=12 答：...

    查看答案和解析>>

    科目：初中数学 来源：2017年吉林省长春市中考数学模拟试卷（7） 题型：单选题

    如图，将等腰直角三角尺ABC绕着点C顺时针旋转到A′B′C的位置，使点A，C，B′在同一条直线上，则旋转角的大小为（　　）

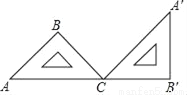
    A. 45° B. 90° C. 120° D. 135°

    D 【解析】∵△ABC为等腰直角三角形， ∴∠A=∠ACB=45°， ∴∠BCB′=180°?45°=135°， ∵等腰直角三角尺ABC绕着点C顺时针旋转到A′B′C的位置， ∴∠BCB′等于旋转角， 即旋转角为135°. 故选：D.

    查看答案和解析>>

    科目：初中数学 来源：山东省2018届九年级12月月考数学试卷 题型：解答题

    如图,A(2,3),B(1,1),C(5,2)以原点O为位似中心,相似比为2, 将△ABC进行变换,画出变换后的图形,并求出相应的坐标.

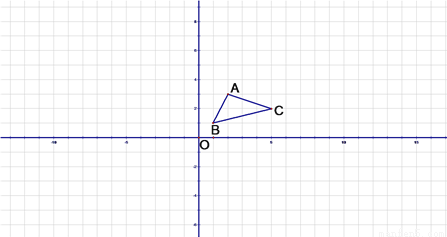
    图形见解析 【解析】若位似比是k，则原图形上的点（x，y），经过位似变化得到的对应点的坐标是（kx，ky）或（-kx，-ky），即可得出A、B、C的对应点的坐标，顺序连接各点即可画出变换出的图形. 【解析】 ∵A(2,3)以原点O为位似中心,相似比为2,将△ABC放大， ∴A的对应点的坐标是(4,6)或(?4,?6) ， B的对应点的坐标是(2,2)或(?2,?2) ， ...

    查看答案和解析>>

    科目：初中数学 来源：山东省2018届九年级12月月考数学试卷 题型：单选题

    在△ABC中，AB＝AC＝3，BC＝2，则6cosB等于 （ ）

    A. 3 B. 2 C. 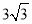D.

    B 【解析】作BC边上的高，利用等腰三角形的性质得BD的长，再利用三角函数定义求解． 【解析】 过点A作AD⊥BC于D. ∵在△ABC中，AB=AC=3，BC=2， ∴BD=DC=1.cosB==， ∴6cosB=6×=2. 故选B.

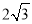
    查看答案和解析>>

    科目：初中数学 来源：江苏省扬州市2016届九年级下学期二模数学试卷 题型：填空题

    如图，AB是⊙O的直径，C是⊙O上一点，OD⊥BC于D，若AC∶BC＝4∶3，AB＝10cm，则OD的长为________cm.

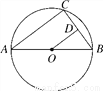
    4 【解析】∵AB是直径， ∴AC⊥BC， 设AC=4x，BC=3x， ∵AC2+BC2=AB2， ∴（4x）2+（3x）2=102， ∴x=2， ∴AC=8cm，BC=6cm， ∵∠ODB=∠ACB，∠B=∠B， ∴△BDO∽△BCA， ∴==， ∴OD=4cm. 故答案为4.

    查看答案和解析>>

    同步练习册答案