
如图,用一个半径为5 cm的定滑轮带动重物上升,滑轮上一点P旋转了108°,假设绳索(粗细不计)与滑轮之间没有滑动,则重物上升了( )
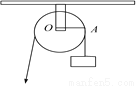
A. π cm B. 2π cm C. 3π cm D. 5π cm
C 【解析】试题分析:根据定滑轮的性质得到重物上升的即为转过的弧长,利用弧长公式得:l==3πcm,则重物上升了3πcm,故选C.科目:初中数学 来源:浙江杭州拱墅区文澜中学2017-2018学年七年级上学期中考试数学试卷(含解析) 题型:单选题
下列计算正确的是( ).
A. 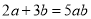 B.
B. 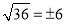 C.
C. 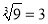 D.
D. 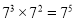
查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题八年级人教版数学试卷(C卷) 题型:填空题
把多项式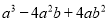 分解因式的结果是_______________.
分解因式的结果是_______________.
查看答案和解析>>
科目:初中数学 来源:黄金30题系列 九年级数学 小题易丢分 题型:填空题
如图所示,在△ABC中,AB=6,AC=4,P是AC的中点,过P点的直线交AB于点Q,若以A、P、Q为顶点的三角形和以A、B、C为顶点的三角形相似,则AQ的长为_____.
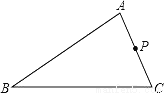
查看答案和解析>>
科目:初中数学 来源:黄金30题系列 九年级数学 小题易丢分 题型:单选题
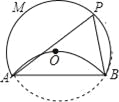
(2015雅安)如图所示,MN是⊙O的直径,作AB⊥MN,垂足为点D,连接AM,AN,点C为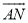 上一点,且
上一点,且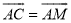 ,连接CM,交AB于点E,交AN于点F,现给出以下结论:①AD=BD;②∠MAN=90°;③
,连接CM,交AB于点E,交AN于点F,现给出以下结论:①AD=BD;②∠MAN=90°;③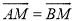 ;④∠ACM+∠ANM=∠MOB;⑤AE=
;④∠ACM+∠ANM=∠MOB;⑤AE=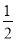 MF.
MF.
其中正确结论的个数是( )
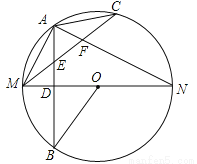
A. 2 B. 3 C. 4 D. 5
D 【解析】根据垂径定理,由AB⊥MN可知AD=DB, ,故①③正确;根据直径所对的圆周角为直角,可由MN为直径,得到∠MAN=90°,故③正确; 如图, 连接OA,由,得到∠MOB=∠MOA=2∠ACM=∠ACM+∠ANM,故④正确; 由, ,可得,所以可得∠AME=∠MAE,根据等角对等边,得到AE=ME,然后根据∠EAF+∠MAE=90°,等量代换得∠EFA+∠AME...查看答案和解析>>
科目:初中数学 来源:黄金30题系列 九年级数学 小题易丢分 题型:单选题
如图,将⊙O沿弦AB折叠,圆弧恰好经过圆心O,点P是优弧 上一点,则∠APB的度数为( )
上一点,则∠APB的度数为( )
A. 45° B. 30° C. 75° D. 60°
D 【解析】作半径OC⊥AB于点D,连结OA,OB, ∵将O沿弦AB折叠,圆弧较好经过圆心O, ∴OD=CD,OD=OC=OA, ∴∠OAD=30°(30°所对的直角边等于斜边的一半),同理∠OBD=30°, ∴∠AOB=120°, ∴∠APB=∠AOB=60°.(圆周角等于圆心角的一半) 故选D.查看答案和解析>>
科目:初中数学 来源:甘肃省武威市2017-2018学年八年级(上)期中数学试卷 题型:解答题
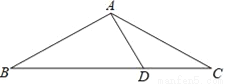
如图,在△ABC中,AB=AC,∠C=30°,AB⊥AD,AD=4cm,求BC的长.
查看答案和解析>>
科目:初中数学 来源:甘肃省武威市2017-2018学年八年级(上)期中数学试卷 题型:单选题
下列各组条件中,能够判定△ABC≌△DEF的是( )
A. ∠A=∠D,∠B=∠E,∠C=∠F B. AB=DE,BC=EF,∠A=∠D
C. ∠B=∠E=90°,BC=EF,AC=DF D. ∠A=∠D,AB=DF,∠B=∠E
C 【解析】试题解析:如图: A、不符合全等三角形的判定定理,即不能推出△ABC≌△DEF,故本选项错误; B、不符合全等三角形的判定定理,即不能推出△ABC≌△DEF,故本选项错误; C、符合直角三角形全等的判定定理HL,即能推出△ABC≌△DEF,故本选项正确; D、不符合全等三角形的判定定理,即不能推出△ABC≌△DEF,故本选项错误; 故选C. ...查看答案和解析>>
科目:初中数学 来源:2017年广东省韶关市南雄市中考数学模拟试卷 题型:单选题
已知二次函数y=ax2+bx+c的图象如图所示,则a、b、c满足( )
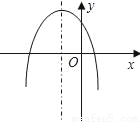
A. a<0,b<0,c>0 B. a<0,b<0,c<0 C. a<0,b>0,c>0 D. a>0,b<0,c>0
A 【解析】试题分析:由于开口向下可以判断a<0,由与y轴交于正半轴得到c>0,又由于对称轴x=-<0,可以得到b<0,所以可以找到结果. 试题解析:根据二次函数图象的性质, ∵开口向下, ∴a<0, ∵与y轴交于正半轴, ∴c>0, 又∵对称轴x=-<0, ∴b<0, 所以A正确.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com