练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

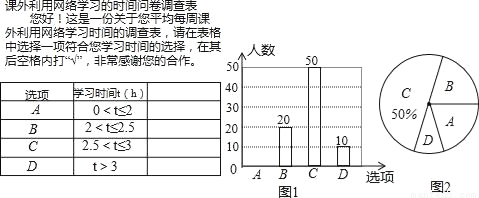
    随着教育信息化的发展，学生的学习方式日益增多，教师为了指导学生有效利用网络进行学习，对学生进行了随机问卷调查（问卷调查表如图所示），并用调查结果绘制了图1、图2两幅统计图（均不完整），请根据统计图解答以下问题：

    （1）本次接受问卷调查的学生共有　 　人，在扇形统计图中“D“选项所占的百分比为　 　；

    （2）扇形统计图中，“B”选项所对应扇形圆心角为　 　度；

    （3）请补全条形统计图；

    （4）若该校共有1200名学生，请您估计该校学生课外利用网络学习的时间在“A”选项的有多少人？

    （1）100，10%；（2）72；（3）补图见解析；（4）240人. 【解析】由条形统计图与扇形统计图获得的数据： 因为图（1）、图（2）中已知C选项的百分比与人数，由C选项的百分比=×100％求解； 先求出B选项的百分比，再利用扇形统计图的圆心角的度数=360°×B选项的百分比求解； （3）由（1）所得总人数求出B选项的人数即可作图； （4）先求出A选项的百分比即可...
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2017年甘肃省兰州市中考数学模拟试卷 题型：填空题

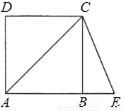
    如图，四边形ABCD是正方形，延长AB到E，使AE=AC，则∠BCE的度数是_____度．

    0.9m 【解析】试题分析：根据正方形的性质，易知∠CAE=∠ACB=45°；等腰△CAE中，根据三角形内角和定理可求得∠ACE的度数，进而可由∠BCE=∠ACE﹣∠ACB得出∠BCE的度数． 【解析】 ∵四边形ABCD是正方形， ∴∠CAB=∠BCA=45°； △ACE中，AC=AE，则： ∠ACE=∠AEC=（180°﹣∠CAE）=67.5°； ∴∠BCE...

    查看答案和解析>>

    科目：初中数学 来源：2017年河北省中考数学模拟试卷 题型：解答题

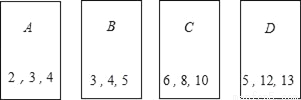
    在四张编号为A，B，C，D的卡片（除编号外，其余完全相同）的正面分别写上如图所示的正整数后，背面向上，洗匀放好．

    （1）我们知道，满足a2+b2=c2的三个正整数a，b，c成为勾股数，嘉嘉从中随机抽取一张，求抽到的卡片上的数是勾股数的概率P1；

    （2）琪琪从中随机抽取一张（不放回），再从剩下的卡片中随机抽取一张（卡片用A，B，C，D表示）．请用列表或画树形图的方法求抽到的两张卡片上的数都是勾股数的概率P2，并指出她与嘉嘉抽到勾股数的可能性一样吗？

    （1）；（2）淇淇与嘉嘉抽到勾股数的可能性不一样． 【解析】试题分析： （1）根据等可能事件的概率的定义，分别确定总的可能性和是勾股数的情况的个数； （2）用列表法列举出所有的情况和两张卡片上的数都是勾股数的情况即可. 试题解析： （1）嘉嘉随机抽取一张卡片共出现4种等可能结果，其中抽到的卡片上的数是勾股数的结果有3种，所以嘉嘉抽取一张卡片上的数是勾股数的概率P1=；...

    查看答案和解析>>

    科目：初中数学 来源：2017年河北省中考数学模拟试卷 题型：单选题

    使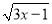有意义的x的取值范围是（　　）

    A. x> B. x>- C. x≥ D. x≥-

    C 【解析】由题意得：3x－1≥0，解得x≥. 故选C.

    查看答案和解析>>

    科目：初中数学 来源：2017年辽宁省营口市大石桥市水源九年一贯制学校中考数学模拟试卷 题型：解答题

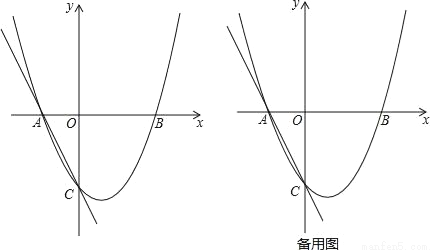
    如图，二次函数y=ax2+bx+c的图象交x轴于A（﹣1，0），B（2，0），交y轴于C（0，﹣2），过A，C画直线．

    （1）求二次函数的解析式；

    （2）点P在x轴正半轴上，且PA=PC，求OP的长；

    （3）点M在二次函数图象上，以M为圆心的圆与直线AC相切，切点为H．

    ①若M在y轴右侧，且△CHM∽△AOC（点C与点A对应），求点M的坐标；

    ②若⊙M的半径为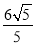，求点M的坐标．

    （1）y=x2﹣x﹣2；（2）；（3）①M（1，﹣2），M′（， ）；②（2，0）或（﹣3，10）． 【解析】（1）根据与x轴的两个交点A、B的坐标，利设出两点法解析式，然后把点C的坐标代入计算求出a的值，即可得到二次函数解析式； （2）设OP=x，然后表示出PC、PA的长度，在Rt△POC中，利用勾股定理列式，然后解方程即可； （3）①根据相似三角形对应角相等可得∠MCH=∠C...

    查看答案和解析>>

    科目：初中数学 来源：2017年辽宁省营口市大石桥市水源九年一贯制学校中考数学模拟试卷 题型：填空题

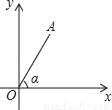
    如图，点A（t，4）在第一象限，OA与x轴所夹的锐角为α，tanα=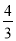，则t的值为_____．

    3 【解析】试题分析：∵点A（t，4）在第一象限，∴AB=4，OB=t，又∵tanα==，∴t=3．故答案为：3．

    查看答案和解析>>

    科目：初中数学 来源：2017年辽宁省营口市大石桥市水源九年一贯制学校中考数学模拟试卷 题型：单选题

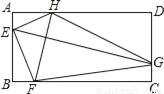
    如图，矩形ABCD中，AD=2AB，E、F、G、H分别是AB，BC，CD，AD边上的点，EG⊥FH，FH=2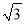，则四边形EFGH的面积为（　　）

    A. 6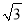 B. 12 C. 12 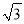D. 24

    B 【解析】过F作FM⊥AD于M，过E作EN⊥CD于N，根据矩形的性质和判定推出EN=2FH，求出EN的长，即可得出答案． 【解析】 过F作FM⊥AD于M，过E作EN⊥CD于N， 则∠FMH=∠ENG=90°， ∵四边形ABCD是矩形，EG⊥FH， ∴∠A=∠D=∠AEN=∠EOF=∠EZF=90°， ∴四边形AEND是矩形， ∴AD=EN， 同理AB=FM， ∵AD=...

    查看答案和解析>>

    科目：初中数学 来源：山东省2018届九年级上期末复习检测数学试卷 题型：填空题

    抛物线y=（x﹣1）2﹣1的顶点在直线y=kx﹣3上，则k=________ ．

    2 【解析】【解析】 ∵抛物线解析式为y=（x﹣1）2﹣1，∴抛物线的顶点坐标为（1，﹣1），∵顶点在直线y=kx﹣3上，∴﹣1=k﹣3，∴k=2．故答案为：2．

    查看答案和解析>>

    科目：初中数学 来源：河北省唐山市路南区2017年中考数学三模试卷（解析版） 题型：单选题

    已知a、b为两个连续的整数，且a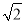＜＜b，则a+b=（   ）

    A. 1                            B. 2                            C. 3                        D. 4

    C 【解析】试题分析：根据二次根式的估算可知： ，则a=1，b=2，a+b=3，故选C．

    查看答案和解析>>

    同步练习册答案