
已知:如图,点E是正方形ABCD中AD边上的一动点,连结BE,作∠BEG=∠BEA交CD于G,再以B为圆心作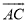 ,连结BG.
,连结BG.
(1)求证:EG与 相切.
相切.
(2)求∠EBG的度数.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:北京市平谷区2018届初三第一学期期末数学试卷 题型:解答题
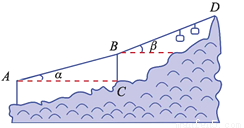
缆车,不仅提高了景点接待游客的能力,而且解决了登山困难者的难题.如图,当缆车经过点A到达点B时,它走过了700米.由B到达山顶D时,它又走过了700米.已知线路AB与水平线的夹角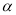 为16°,线路BD与水平线的夹角β为20°,点A的海拔是126米.求山顶D的海拔高度(画出设计图,写出解题思路即可).
为16°,线路BD与水平线的夹角β为20°,点A的海拔是126米.求山顶D的海拔高度(画出设计图,写出解题思路即可).
查看答案和解析>>
科目:初中数学 来源:安徽省六安市2018届九年级上学期第二次月考数学试卷 题型:单选题
下列命题:(1)经过三点一定可以作圆;(2)任一个三角形一定有一个外接圆,而且只有一个外接圆;(3)任意一个圆一定有一个内接三角形,而且只有一个内接三角形;(4)三角形的外心到三角形三个顶点的距离相等.上述结论中正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
B 【解析】根据在同一平面内,经过不在同一直线上的三点,确定一个圆,可知(1)不正确,(2)正确;任意一个圆有无数个内接三角形,(3)不正确;三角形的外心是三角形三条垂直平分线的交点,所以到三角形三个顶点的距离相等,故(4)正确. 故选:B.查看答案和解析>>
科目:初中数学 来源:上海浦东新区2017-2018学年九年级上学期期末数学试卷(初三一模) 题型:填空题
计算:3tan30°+sin45°= .
【解析】3tan30°+sin45°==. 故答案为:查看答案和解析>>
科目:初中数学 来源:上海浦东新区2017-2018学年九年级上学期期末数学试卷(初三一模) 题型:单选题
已知非零向量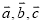 ,下列条件中,不能判定向量
,下列条件中,不能判定向量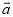 与向量
与向量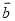 平行的是
平行的是
A. 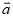 ∥
∥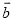
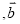 ∥
∥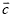 B.
B. 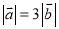 C.
C. 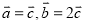 D.
D. 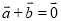
查看答案和解析>>
科目:初中数学 来源:云南省2018届九年级上学期期中考试数学试卷 题型:解答题
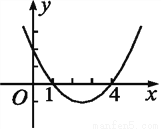
已知二次函数y=ax2-5x+c的图象如图所示.
(1)试求该二次函数的解析式和它的图象的顶点坐标;
(2)观察图象回答,x何值时y的值大于0?
查看答案和解析>>
科目:初中数学 来源:云南省2018届九年级上学期期中考试数学试卷 题型:填空题
点A的坐标是(-6,8),则点A关于x轴对称的点的坐标是_________,点A关于y轴对称的点的坐标是_________,点A关于原点对称的点的坐标是_________.
(-6,-8) (6,8) (6,-8) 【解析】【解析】 ∵在平面直角坐标系中,点关于x轴对称时,横坐标不变,纵坐标为相反数,∴点A关于x轴对称的点的坐标是(﹣6,8),∵关于y轴对称时,横坐标为相反数,纵坐标不变,∴点A关于y轴对称的点的坐标是(6,8),∵关于原点对称时,横纵坐标都为相反数,∴点A关于原点对称的点的坐标是(6,﹣8),故答案为:(﹣6,8),(6,8),(6,﹣8)....查看答案和解析>>
科目:初中数学 来源:2017-2018学年度第一学期海南省海口市九年级数学科期末检测题 题型:解答题
学校课外生物小组的试验园地是长35米、宽20米的矩形,为便于管理,现要在中间开辟一横两纵三条等宽的小道(如图),要使种植面积为600平方米,求小道的宽.若设小道的宽为x米,则可列方程为 .

查看答案和解析>>
科目:初中数学 来源:内蒙古赤峰市宁城县2017-2018学年八年级上学期期末考试数学试卷 题型:解答题
探究归纳题:
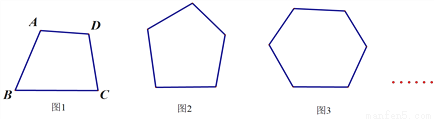
(1)试验分析:
如图1,经过A点可以做__________条对角线;同样,经过B点可以做__________条;经过C点可以做__________条;经过D点可以做__________条对角线.
通过以上分析和总结,图1共有___________条对角线.
(2)拓展延伸:
运用(1)的分析方法,可得:
图2共有_____________条对角线;
图3共有_____________条对角线;
(3)探索归纳:
对于n边形(n>3),共有_____________条对角线.(用含n的式子表示)
(4)特例验证:
十边形有__________________对角线.
1 1 1 1 2 5 9 35 【解析】试题分析:(1)根据对角线的定义,四边形经过任意一点可以做1条对角线,其中会出现重复,因此四边形共有2条对角线,(2)五边形经过任意一点可以做2条对角线,其中会出现重复,因此四边形共有5条对角线, 六边形经过任意一点可以做3条对角线,其中会出现重复,因此四边形共有9条对角线,(3) n边形经过任意一点可以做(n-3)条对角线,其中会出现重复,因此四边...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com