
探究归纳题:
(1)试验分析:
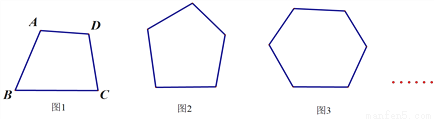
如图1,经过A点可以做__________条对角线;同样,经过B点可以做__________条;经过C点可以做__________条;经过D点可以做__________条对角线.
通过以上分析和总结,图1共有___________条对角线.
(2)拓展延伸:
运用(1)的分析方法,可得:
图2共有_____________条对角线;
图3共有_____________条对角线;
(3)探索归纳:
对于n边形(n>3),共有_____________条对角线.(用含n的式子表示)
(4)特例验证:
十边形有__________________对角线.
1 1 1 1 2 5 9 35 【解析】试题分析:(1)根据对角线的定义,四边形经过任意一点可以做1条对角线,其中会出现重复,因此四边形共有2条对角线,(2)五边形经过任意一点可以做2条对角线,其中会出现重复,因此四边形共有5条对角线, 六边形经过任意一点可以做3条对角线,其中会出现重复,因此四边形共有9条对角线,(3) n边形经过任意一点可以做(n-3)条对角线,其中会出现重复,因此四边... 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:初中数学 来源:云南省2018届九年级上学期期中考试数学试卷 题型:解答题
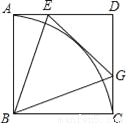
已知:如图,点E是正方形ABCD中AD边上的一动点,连结BE,作∠BEG=∠BEA交CD于G,再以B为圆心作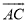 ,连结BG.
,连结BG.
(1)求证:EG与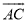 相切.
相切.
(2)求∠EBG的度数.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年度第一学期海南省海口市九年级数学科期末检测题 题型:单选题
将一元二次方程x2-6x-5=0化成(x+a)2=b的形式,则b等于( )
A. -4 B. 4 C. -14 D. 14
D 【解析】试题解析: 故选D.查看答案和解析>>
科目:初中数学 来源:安徽省2017-2018学年度七年级第一学期人教版数学期末自测试卷(二) 题型:单选题
在同一平面上,若∠BOA=60.3°,∠BOC=20°30′,则∠AOC的度数是( )
A. 80.6° B. 40° C. 80.8°或39.8° D. 80.6°或40°
C 【解析】分两种情况考虑:如图1与图2所示,分别求出∠AOC的度数即可. 【解析】 分两种情况考虑: (1)如图1所示,此时∠AOC=∠AOB-∠BOC=60.3°-20°30′=39.8°; (2)如图2所示,此时∠AOC=∠AOB+∠BOC=60.3°+20°30′=80.8°, 综上,∠AOC的度数为39.8°或80.8°. 故选C “点睛”此题考查了角的计...查看答案和解析>>
科目:初中数学 来源:安徽省2017-2018学年度七年级第一学期人教版数学期末自测试卷(二) 题型:单选题
若使等式(-4)□(-6)=2成立,则□中应填入的运算符号是( )
A. + B. - C. × D. ÷
B 【解析】利用运算法则计算即可确定出运算符号. 【解析】 根据题意得,(-4)-(-6)=-4+6=2, 故选B.查看答案和解析>>
科目:初中数学 来源:内蒙古赤峰市宁城县2017-2018学年八年级上学期期末考试数学试卷 题型:解答题
先化简再求值: 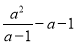 ,其中a=2
,其中a=2
查看答案和解析>>
科目:初中数学 来源:内蒙古赤峰市宁城县2017-2018学年八年级上学期期末考试数学试卷 题型:单选题
已知:2+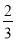 =22×
=22×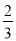 ;3+
;3+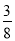 =32×
=32×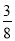 ;4+
;4+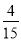 =42×
=42×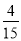 ;5+
;5+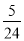 =52×
=52×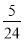 …,若10+
…,若10+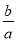 =102×
=102×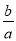 符合前面式子的规律,则a+b=( )
符合前面式子的规律,则a+b=( )
A. 99 B. 109 C. 100 D. 120
B 【解析】根据题目中的等式可归纳出式子的规律:等式中分数的分母等于式子中第一个整数的平方减1,分子等于第一个整数,所以a=99,b=10,故选B.查看答案和解析>>
科目:初中数学 来源:辽宁省2018届九年级(上)期末模拟数学试卷 题型:解答题
如图1,点I是△ABC的内心,AI的延长线交△ABC的外接圆⊙O于点D.
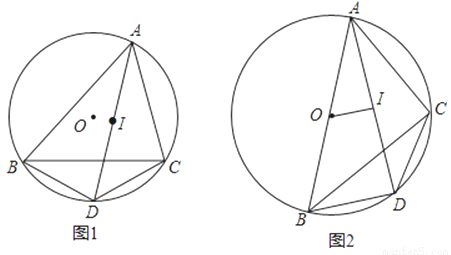
(1)求证:DB=DC=DI;
(2)若AB是⊙O的直径,OI⊥AD,求tan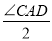 的值.
的值.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期初三数学期末试卷 题型:单选题
某校科技实践社团制作实践设备,小明的操作过程如下:
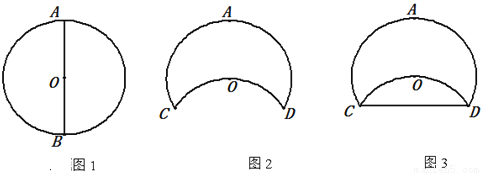
①小明取出老师提供的圆形细铁环,先通过在圆一章中学到的知识找到圆心O,再任意找出圆O的一条直径标记为AB(如图1),测量出AB=4分米;
②将圆环进行翻折使点B落在圆心O的位置,翻折部分的圆环和未翻折的圆环产生交点分别标记为C、D(如图2);
③用一细橡胶棒连接C、D两点(如图3);
④计算出橡胶棒CD的长度.
小明计算橡胶棒CD的长度为( )
A. 2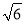 分米 B. 2
分米 B. 2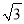 分米 C. 3
分米 C. 3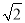 分米 D. 3
分米 D. 3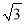 分米
分米
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com