
��ͼ����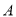 ��
��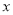 ���ϣ�
���ϣ� 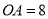 �����߶�
�����߶�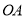 �Ƶ�
�Ƶ�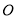 ˳ʱ����ת
˳ʱ����ת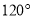 ��ʹ��
��ʹ��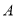 ���
���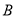 �غ�.
�غ�.
��1�����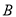 �����ꣻ
�����ꣻ
��2����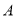 ��
��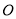 ��
��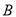 ����������ߵĽ���ʽ��
����������ߵĽ���ʽ��
��3���ڴ������ߵĶԳ����ϣ��Ƿ���ڵ�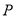 ��ʹ���Ե�
��ʹ���Ե�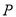 ��
��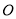 ��
��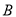 Ϊ������������ǵ��������Σ������ڣ������
Ϊ������������ǵ��������Σ������ڣ������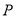 �����꣺�������ڣ���˵������.
�����꣺�������ڣ���˵������.

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ���˽̰���꼶�ϲ���ѧ 22.3ʵ����������κ�����3������ ���ͣ���ѡ��
С���ڽ����У�˶�����Զ����������������һ��������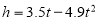 ���ĵ�λ���룬
���ĵ�λ���룬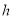 �ĵ�λ���ף�������������Ծʱ���ĸ߶ȵı仯�������������������ʱ���õ�ʱ���ǣ�������
�ĵ�λ���ף�������������Ծʱ���ĸ߶ȵı仯�������������������ʱ���õ�ʱ���ǣ�������
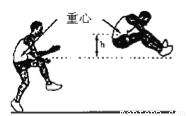
A.0.71s����B.0.70s������C.0.63s������D.0.36s
D �������� ������������κ������䷽�� .�����������.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���˽̰���꼶�ϲ���ѧ 22.1.3���κ���ya��x-h��2+k��ͼ������ʣ�3������ ���ͣ������
������y��3(x��2)2�Ŀ��ڷ�����______����������Ϊ______���Գ�����______����x______ʱ��y��x�����������x��______ʱ��y����______ֵ��______����������������y��3x2��______ƽ��______����λ�õ���
���� (2��0) ֱ��x�� 2 ��2 2 С 0 �� 2�� ���������������� ������y��3��x��2��2�Ŀ��ڷ��������ϣ���������Ϊ��2��0�����Գ�����ֱ��x�� 2����x��2ʱ��y��x�����������x��2ʱ��y����Сֵ��0����������������y��3x2����ƽ��2����λ�õ��� �ʴ�Ϊ�����ϣ� ��2��0���� ֱ��x�� 2����2 ��2��С�� 0�� �ң�2���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���˽̰���ѧ���꼶�ϲ� ��11�� 11.3.1 �����ͬ����ϰ�������棩 ���ͣ���ѡ��
���һ���ı��ε�������õ������������Խ��߳˻���һ�룬��ô����ı���һ���ǣ� ��
A. ���� B. ���� C. ������ D. �Խ����ഹֱ���ı���
D �����������һ���ı��ε�������õ������������Խ��߳˻���һ�룬��ô����ı���һ���ǶԽ����ഹֱ���ı��Σ���ѡD.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���˽̰���ѧ���꼶�ϲ� ��11�� 11.3.1 �����ͬ����ϰ�������棩 ���ͣ���ѡ��
������ε�һ�����㣬�����������Խ��ߣ� ��
A. 2 B. 3 C. 4 D. 5
A ������������n���δ�һ�����������������n-3�����Խ��߿�ֱ�ӵõ� ������ε�һ�������������5?3=2���Խ��ߣ� ��ѡA.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�����Ĵ����ص�����ѧ���꼶�ڶ��ν��Կ�����ѧ�Ծ� ���ͣ������
��֪����x��һԪ���η���x2 + 2(k��1)x + k2��1 = 0����������ȵ�ʵ������
(1)��ʵ��k��ȡֵ��Χ��
(2)0�����Ƿ��̵�һ���������ǣ������������һ�����������ǣ���˵�����ɣ�
��1��k��1����2����һ������4�� �������������������1����������������ȵ�ʵ���������������=b2��4ac��0���ɴ˿��Եõ�����k�IJ���ʽ��Ȼ��ⲻ��ʽ�������ʵ��k��ȡֵ��Χ�� ��2�����ü���ķ��������������һ������ �����������1���ߡ�=[2��k��1��]2��4��k2��1�� =4k2��8k+4��4k2+4=��8k+8�� �֡�ԭ��������������ȵ�ʵ������ ...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�����Ĵ����ص�����ѧ���꼶�ڶ��ν��Կ�����ѧ�Ծ� ���ͣ������
������ͳ��ͼ��ӳ������½���뺣����ռ�ı���ʱ����½�ء����ֶ�Ӧ��Բ�Ľ���108�㣮������һ����ʯ���ڵ����ϣ�����½�صĸ����� ��
0.3 �������� �����������½�ء����ֶ�Ӧ��Բ�Ľ���108�㣮������һ����ʯ���ڵ�������Բ�Ľǣ��ϣ�����½�صĸ���=�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2016������꼶��ѧ�ϲᣨ�˽̰棩11��2.2�����ε������ϰ�����𰸣� ���ͣ�
��ͼ��ʾ,��ABC,��ACB���ڽ�ƽ���߽��ڵ�O,��ABC ���ڽ�ƽ�������ACB�����ƽ���߽��ڵ�D,��ABC���ACB���������ƽ���߽��ڵ�E,�ҡ�A=60��, ���BOC=_______,��D=_____,��E=________.
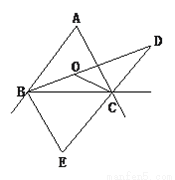
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���˽̰���꼶�ϲ���ѧ 22.1.4���κ���yax2+bx+c��ͼ������ʣ�1����ϰ ���ͣ���ѡ��
��ƽ��ֱ������ϵ�У����������y��2x2����������x�ᡢy��ֱ����ϡ�����ƽ��2����λ����ô��������ϵ�������ߵĽ���ʽ��
A��y��2(x��2)2 + 2 B��y��2(x + 2)2��2
C��y��2(x��2)2��2 D��y��2(x + 2)2 + 2
B ��������������ƽ�Ʋ��ı�a��ֵ���������Ĺؼ��ǵõ��������ߵĶ������꣮ �������� �Ƚ�x�ᡢy���ƽ��ת��Ϊ�����ߵ�ƽ�ƣ����ɿ�������������x�᷽������ƽ��2����λ���ȣ���y�᷽������ƽ��2����λ���ȣ�ԭ�����ߵĶ���Ϊ��0��0��������ƽ��2����λ��������ƽ��2����λ����ô�������ߵĶ���Ϊ��-2��-2���������������ߵĽ���ʽΪy=2��x-h��2+k������ã�y=2��x+2��2-2...�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com