
��ƽ��ֱ������ϵ�У����������y��2x2����������x�ᡢy��ֱ����ϡ�����ƽ��2����λ����ô��������ϵ�������ߵĽ���ʽ��
A��y��2(x��2)2 + 2 B��y��2(x + 2)2��2
C��y��2(x��2)2��2 D��y��2(x + 2)2 + 2
B ��������������ƽ�Ʋ��ı�a��ֵ���������Ĺؼ��ǵõ��������ߵĶ������꣮ �������� �Ƚ�x�ᡢy���ƽ��ת��Ϊ�����ߵ�ƽ�ƣ����ɿ�������������x�᷽������ƽ��2����λ���ȣ���y�᷽������ƽ��2����λ���ȣ�ԭ�����ߵĶ���Ϊ��0��0��������ƽ��2����λ��������ƽ��2����λ����ô�������ߵĶ���Ϊ��-2��-2���������������ߵĽ���ʽΪy=2��x-h��2+k������ã�y=2��x+2��2-2...
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2017�����Ĵ����ص�����ѧ���꼶�ڶ��ν��Կ�����ѧ�Ծ� ���ͣ������
��ͼ����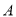 ��
��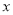 ���ϣ�
���ϣ� 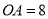 �����߶�
�����߶�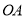 �Ƶ�
�Ƶ� ˳ʱ����ת
˳ʱ����ת ��ʹ��
��ʹ�� ���
���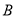 �غ�.
�غ�.
��1�����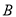 �����ꣻ
�����ꣻ
��2����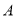 ��
��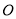 ��
��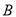 ����������ߵĽ���ʽ��
����������ߵĽ���ʽ��
��3���ڴ������ߵĶԳ����ϣ��Ƿ���ڵ�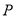 ��ʹ���Ե�
��ʹ���Ե�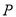 ��
��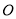 ��
��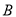 Ϊ������������ǵ��������Σ������ڣ������
Ϊ������������ǵ��������Σ������ڣ������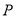 �����꣺�������ڣ���˵������.
�����꣺�������ڣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ�Ϸ�����У2017-2018ѧ����꼶��ѧ�����п�����ѧ�Ծ� ���ͣ������
С�۸���ѧϰ�����ľ��飬�Ժ���y=|x��1|��ͼ�������ʽ�����̽����������С�۵�̽�����̣��벹����ɣ�
��1������y=|x��1|���Ա���x��ȡֵ��Χ���� ����
��2���б����ҳ�y��x�ļ����Ӧֵ��
x | �� | ��1 | 0 | 1 | 2 | 3 | �� |
y | �� | b | 1 | 0 | 1 | 2 | �� |
����b=�� ����
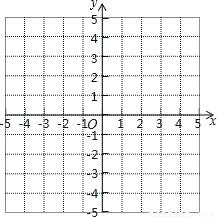
��3����ƽ��ֱ������ϵxOy�У�������ϱ��и��Զ�ӦֵΪ����ĵ㣬�������ú�����ͼ��
��4��д���ú�����һ�����ʣ��� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ�Ϸ�����У2017-2018ѧ����꼶��ѧ�����п�����ѧ�Ծ� ���ͣ���ѡ��
���ں���y=2x��1������˵����ȷ���ǣ�������
A. ����ͼ����㣨1��0�� B. yֵ����xֵ�������С
C. ����ͼ���ڶ����� D. ��x��1ʱ��y��0
D ����������������ͼ��ѡ��A, �㣨1��0�����뺯���� ������. ��ͼ��֪��B��C����D,��ȷ. ѡD.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���˽̰���꼶�ϲ���ѧ 22.1.4���κ���yax2+bx+c��ͼ������ʣ�1����ϰ ���ͣ���ѡ��
��֪������y��ax2��bx��c(a<0)��A(��2��0)��O(0��0����B(��3��y1)��C(3��y2)�ĵ㣬��y1 ��y2�Ĵ�С��ϵ��
A. y1��y2 B. y1=y2 C. y1��y2 D. ����ȷ��
A ���������������߹�A(?2,0)��O(0,0)���㣬 �������ߵĶԳ���Ϊx==?1�� ��a<0�������߿������£���Գ���ԽԶ������ֵԽС�� �ȽϿ�֪D����Գ���Զ����Ӧ��������ֵС�� ��y₁>y₂����ѡA.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���˽̰���꼶�ϲ���ѧ 22.1.4���κ���yax2+bx+c��ͼ������ʣ�1����ϰ ���ͣ���ѡ��
��֪���κ���y=ax2+bx+c��x��y�IJ��ֶ�Ӧֵ���±���
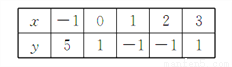
��ö��κ���ͼ��ĶԳ���Ϊ( )
A. y�� B. ֱ��x=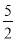 C. ֱ��x=2 D. ֱ��x=
C. ֱ��x=2 D. ֱ��x=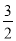
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����һ��ѧ��һѧ��6.1���ݵ��ռ� ͬ����ϰ ���ͣ������
ij������36����ѧ�����о��꼶ѧ����7000����Ϊ���˽�õ������꼶ѧ�����������������������ѧ��ͳ��֪ʶ�����������������Ҫ�����ļ�����Ҫ����������ٳ������飻����Ƶ����ʾ������������������壻���������ݣ��ݷ������ݣ�����_____��ֻд��ţ�
�ڢ٢ܢݢۣ� �����������һ��������Ҫ�����ļ�����Ҫ����Ϊ������Ƶ����ʾ����ٳ������飻���������ݣ��ݷ������ݣ����������������壬 �ʴ�Ϊ���ڢ٢ܢݢۣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���˽̰���꼶�ϲ���ѧ 23.2.3����ԭ��ԳƵĵ������ ��ϰ ���ͣ������
��֪��A(2a+2��3-3b)���B(2b-4��3a+6)��������ԭ��Գƣ���a��b��ֵ.
a=-1��b=2. ���������������������ԭ��Գƺ�ĺ������궼��Ϊ�෴�������������г�����a��b�Ķ�Ԫһ�η����飬�Ӷ����a��b��ֵ�� ����������������⣬��(2a+2)+(2b-4)=0�� (3-3b)+(3a+6)=0�� ��ã�a=-1��b=2���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�����˽̰���ѧ���꼶�ϲ� ��23�� ��ת ȫ�²��Ծ� ���ͣ������
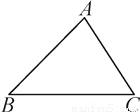
��ͼ���ڡ�ABC�У���B��45�㣬��C��60�㣬����ABC�Ƶ�A��ת30���õ���AB1C1�����BAC1�Ķ�����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com